资金的时间价值(卷名：水利)
time value of funds
资金经合理运用一定时间后，所具有的赢利增值的潜在能力。利率越高、时间越长，所赢得的利润及增值也越多，一般以复利公式加以计算。现在拥有的一定数量的资金，等价于若干年后更大数量的一笔资金；同理，若干年后的一笔资金，折算为现值时要打一折扣。一年后的资金折算为现在的资金时所打的折扣，称为折现率。由于水利工程的寿命一般很长，在寿命期内还要确定一个为期30～50年的经济分析期。在此期中每年都可能投入或回收一定的资金。为了比较各方案的经济效率，需要将不同年份的资金按其时间价值折算为同一时间的资金值。
资金流程图 为了直观清晰地表达某项水利工程各年投入的费用和取得的收益，可以绘制资金流程图（图1）。图中的横坐标为时间，每小格表示1年；纵坐标为资金，箭头长度按一定比例表示资金数值，箭头向上的为收入，向下的为支出。一般以工程完工并开始投入运行之年的年初作为原点（基点），原点左边各年是施工期，原点右边各年是运行期。为简便起见，一般都把各年的收支金额当作是集中在年末发生的。从图上可以很容易看出，第一年的年末就是第二年的年初。
不同时资金的相互折算 根据复利计算原理对不同年份的资金，可按下列方法进行相互折算。
一次整付折算 资金P在第一年初开始使用，如年利率为i，在使用期中不取出利息，则到n年末所一次整付的本利和F值应为：
F =P（1+i）n (1)式中P为现值；F为终值；(1+i)n为一次整付终值因子并用符号（F／P，i，n）表示。亦即现在的P元，可折算为n年末的P(1+i)n元。
当已知终值F，要折算为现值P时，可用下式计算：
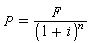(2)式中
为一次整付现值因子，用符号(P/F，i，n)表示。
均等年金折算 如在 n年的每年末均存入一相等的年金A值（图2），年利率为i，则到n年末所得本利和F为:
(3)式中
为均等年金本利因子，可用符号(F/A，i，n)表示。如已知F，要折算为各年年金为A的n年均等系列，则可用下式计算：
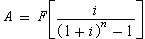(4)式中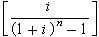
为偿债基金因子，用(A/F，i，n)表示。其含意为如某人拟在n年末偿还1元的债务，当年利率为i时，应在n年中的每年末支付(A/F，i，n)金额。将均等年金系列换算为相应的现值P时，可用下式：
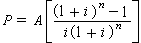(5)式中
为均等年金现值因子， 用(P/A，i，n)表示。其含意是，如在n年中的每年末要提取1元钱，且年利率为i时，在开始时应投入的资金数值。将现值P换算为等价的均等年金系列时，可用下式：
(6)式中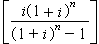
为资本回收因子，用符号 (A/P，i，n)表示。其含意为开始投入1元钱，当利率为i时，在n年的每年末可以提取的钱数。
递增等差年金折算 如在n 年内每年年末的收入不是均等的，而是随着工程的逐渐完善而成等差级数递增的，就成为一个递增等差年金系列（图3）。在第一年末收支的金额为0，第二年末的金额为G，第3年末的金额为2G，如此类推，在Π年末的金额为(n-1)G，各年的级差为G。
这一递增等差年金系列可按下式折算成现值P:
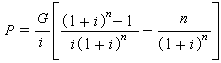(7)也可按下式折算为均等年金系列的A:
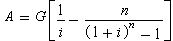(8)式中
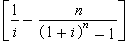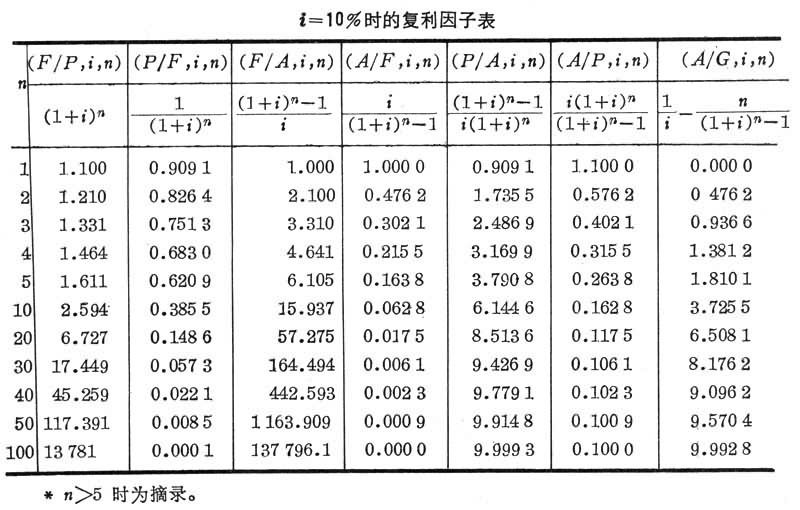
为递增转换因子，用符号(A/G，i，n)表示。用此因子将递增等差年金系列转换成一个均等年金系列后，即可利用上面的(3)(4)(5)(6)各式，进行资金的各种折算。复利因子表 上列公式(1)(2)(3)(4)(5)(6)(8)中的各种复利因子，均已按不同的利率i和年数n，制成复利因子表（见表），加以查用，可使计算十分简捷。
水利工程寿命 包括物理寿命和经济寿命两方面。
①物理寿命：从水利工程或某项设施建成至不能使用为止的一个期限，又称实际寿命。
②经济寿命:从某项水利工程或设施投入使用起，至一定年数后，由于效益降低、运行维修费用增加或高效能新产品的问世，以致再继续使用原设施不如重新建造或购置更新，更为经济。这时，这种设施的经济寿命就结束了。随着科学技术的进步，同等效能设施的建造费和运行维修费往往比以前降低，因此经济寿命就会缩短。不易损坏的耐用建筑物的经济寿命很长，而机电设备的经济寿命一般较短。可根据更新重置的经济分析，对水利工程的经济寿命加以确定。
经济分析期 在工程的经济寿命期内，选定一个期限作为各方案共同的经济分析期。这一期限应有足够的长度，使各方案的有利和不利的经济、环境和社会方面的效果均能充分显示出来，并达到相对稳定的程度，从而使各方案之间具有比较一致的可比条件。
一般大型水利工程的经济分析期可以采用50年。如果某一方案的经济寿命短于共同的经济分析期时，则可以在它的寿命终了时进行更新重置，以便与经济寿命较长的方案进行比较。如果某工程方案的经济寿命长于经济分析期，则应计算该方案在经济分析期终了时所保有的残值。