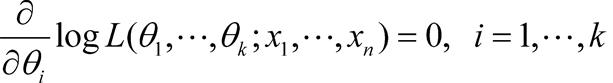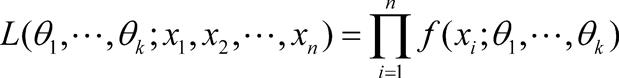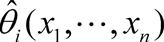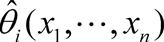| 释义 |
最大似然估计 最大似然估计数理统计中一种重要而常用的参数估计。它的基本思想是构造一个样本的函数去估计未知参数,当比较不同参数下样本观测值出现的可能性时,最大似然估计使样本观测值出现的可能最大。正态分布N(μ,σ2)中的两个参数μ与σ2的最大似然估计分别是样本均值=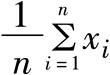 和样本方差 和样本方差出处:数理化力学卷 • 数 学 • 概率论 • 数理统计 最大似然估计 参数估计中的一种常用方法。最大似然估计法的直观思想是:设(x1,x2,…,x n)是抽自总体X的样本观察值,总体X的分布中含未知参数,既然在一次试验中出现的结果为(x1,x2,…,x n),那么应该选取这样的值作为未知参数的估计,使得出现这一结果的概率达最大。使似然函数达到最大值的统计量。设总体X的概率分布或密度函数为f(x;θ1,…,θ k),(θ1,…,θ k)是待估未知参数,记 , 称它为似然函数,它是(X1,X2,…,Xn)的联合概率分布或联合密度函数。根据最大似然原理,只需求出使得L(θ1,…,θk;x1,x2,…,xn)达到最大值的作为θi的估计,称这样的为参数θi(i=1,…,k)的最大似然估计值,用(X1,X2,…,Xn)替代(x1,x2,…,xn),称 或(X1,…,Xn)为θi(i=1,…,k)的最大似然估计量。当似然函数可微时,可借助于微分在使似然函数的偏导数(或导数)为0的点中找出似然函数的最大值点,而称 为似然方程。最大似然估计在理论上有优良的性质,如在很一般的条件下,最大似然估计是渐近正态和渐近有效的。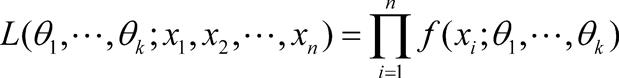 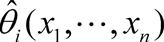 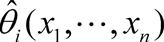 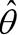 出处:管理学卷 • 统 计 学 • 数理统计 |
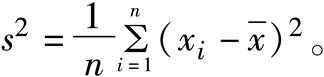
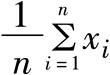 和样本方差
和样本方差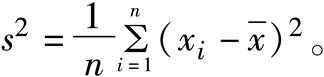
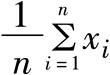 和样本方差
和样本方差