in linear and multilinear algebra, procedure for solving systems of simultaneous linear equations by means of determinants (see also determinant; linear equation). Although Cramer's rule is not an effective method for solving systems of linear equations in more than three variables, it is of use in studying how the solutions to a system AX=B depend on the vector B. If

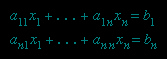
is a system of n simultaneous linear equations in n unknowns, then a solution of this system is

in which det A is the determinant of the matrix A (in which the elements of each row are the coefficients a_ij of one of the equations) and the matrix B_i is formed by replacing the ith column of A by the column of constants b₁,…, b_n.

If det A equals zero, the system has no unique solution; that is, there is no set x₁,…, x_n that satisfies all of the equations.