Laplace transform
mathematics
in mathematics, a particular integral transform invented by the French mathematician Pierre-Simon Laplace (Laplace, Pierre-Simon, marquis de) (1749–1827), and systematically developed by the British physicist Oliver Heaviside (Heaviside, Oliver) (1850–1925), to simplify the solution of many differential equations (differential equation) that describe physical processes. Today it is used most frequently by electrical engineers in the solution of various electronic circuit problems.
The Laplace transform f(p), also denoted by L{F(t)} or Lap F(t), is defined by the integral
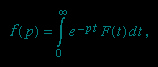
involving the exponential (exponential function) parameter p in the kernel K=e−pt. The linear Laplace operator L thus transforms each function F(t) of a certain set of functions into some function f(p). The inverse transform F(t) is written L−1{f(p)} or Lap−1f(p).
- Sanjay Gupta
- San Joaquin River
- San Jose
- San Jose scale
- San José
- San José de las Lajas
- San José del Guaviare
- San Juan
- San Juan Bautista
- San Juan Capistrano
- San Juan del Monte
- San Juan de los Morros
- San Juan Islands
- San Juan Mountains
- San Juan River
- San Justo
- Sanjō
- Sanjō, Go-
- Sanjō Sanetomi
- Sanka
- Sankaran Nair, Sir Chettur
- sankin kōtai
- Sankt Gallen
- Sankt Johann
- Sankt Michael