德拜模型(卷名：物理学)
Debye model
P.J.W.德拜提出的计算固体热容的原子振动模型。1912年，德拜改进了爱因斯坦模型，考虑热容应是原子的各种频率振动贡献的总和，得到了同实验结果符合得很好的固体热容公式。
德拜模型把原子排列成晶体点阵的固体看作是一个连续弹性媒质，原子间的作用力遵从胡克定律，组成固体的 N个原子在三维空间中集体振动的效果相当于3N个不同频率的独立线性振子的集合。每一个独立谐振子的振动是一种简正振动模式，弹性媒质的一种简正振动模式是具有一定频率、波长和传播方向的弹性波。弹性固体能够以不同的速度传播纵、横两种波。对于每一个振动频率，纵波只有在传播方向的一种振动，横波有两种垂直于传播方向的振动（两个偏振），共三个振动模式。为把固体看作是连续的弹性媒质，德拜模型只考虑那些频率非常低（近似取为零）直到极限频率vm范围内的振动模式。由于N的数目很大，3N种振动频率可看作是连续分布在零到vm区间内，则3N个不同频率的独立谐振子的总能量就由分立的求和变为积分
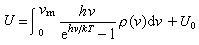，Uo是同温度无关的常数， ρ(v)称频率分布函数。用热力学关系
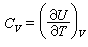，由点阵振动导致的固体的定容热容是 
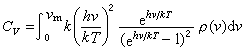。ρ(v)的形式是
其中V是固体的体积，с1、сt分别是固体中纵波和横波的传播速度。由条件
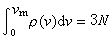可得到德拜最大频率是
，而ρ(v)就可写成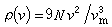
。令x=hv/kT， 便导出了固体的摩尔热容
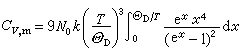，其中嘷D＝hvm/k称德拜温度。上式在T
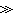嘷D时导出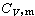
＝3R(R是摩尔气体常数)，就是经典结果；当T
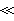嘷D时，可得
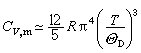，随着T→0，
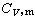按T3趋于零。对中间温度区域，则需用数值计算求积分值。对于一些简单结构的固体，其热容的理论曲线同实验结果的比较见图。图中同时画出了杜隆-珀替定律的曲线（图中虚线）。可见，德拜模型导出的热容公式同实验符合得很好。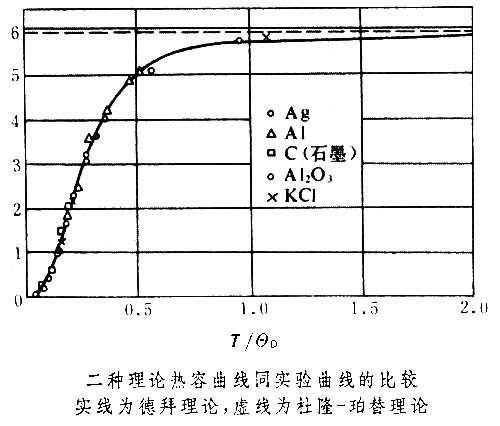
根据量子论，德拜所考虑的弹性波的简正振动能量也是量子化的，是最小能量hv的倍数。弹性波的这一最小能量称为声子，它是固体原子系统的集体激发模式，可看作是在点阵中传播的具有一定能量和运动方向的准粒子。把弹性声波场当作声子系统处理后，再把普朗克公式运用到固体点阵振动上，频率为v的振子振动的平均能量就是
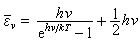，那么3N个不同频率的独立谐振子的总能量是各振子平均能量的和。德拜模型不能用于以下几种情况：①较复杂的分子，特别是高度各向导性晶体，前述的频率分布函数不适用时；②波长同点阵间距离可比拟，破坏了连续媒质的设想时；③极低温度下，电子参与对热容贡献并起主要作用时（见电子比热容）。