热力学第三定律(卷名：物理学)
third law of thermodynamics
研究当温度趋于绝对零度时物质性质的热力学定律。用热力学第二定律的公式
确定熵时，留下一个常数无法确定。但已知许多物理、化学现象和此常数有重要关系。热力学第三定律解决了确定熵常数的问题。在等压条件下的化学反应热Q和化学亲合势A有下列关系：
即
式中Q是系统经等压过程吸收的热量，它等于系统的焓变Q＝-ΔH；A是化学亲合势，它等于吉布斯函数的减小量A＝-ΔG。大量实验结果表明:当温度趋于绝对零度时，化学亲合势和反应热相等，并且当T→0时，Q-A这个量趋于零的速度比T的一次方趋于零的速度快，即有关系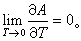
从热力学关系
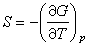很自然得到
此式就是W.能斯脱在研究低温下各种化学反应性质时，总结大量实验资料于1906年提出的一个普遍规律，称为能斯脱定理。表述为：凝聚系的熵在等温过程中的改变随热力学温度趋于零。这个定理后来称为热力学第三定律。由能斯脱定理可推出另一原理：“不可能用有限手续使一物体冷却到绝对温度的零度”，这个原理叫做绝对零度不能达到原理。它是热力学第三定律的另一种表述。后来人们发现，能斯脱定理只适用于晶体，对非晶体不适用，而绝对零度不能达到原理则更具有普遍性，所以把绝对零度不能达到原理作为热力学第三定律的标准说法，而把能斯脱定理作为它的推论。
1911年M.普朗克提出绝对熵的概念，即规定绝对零度时熵本身等于零，而不是熵的改变等于零，即
在这样规定之后，熵的数值中就不再包含任意常数了。绝对熵的说法可以代替能斯脱定理，且更为简单。在第三定律建立之前，计算熵的普遍公式为
其中So为标准温度To时熵的数值，So是参量x（x可代表体积、压强等）的函数，Cx为热容，根据第三定律，取T＝0为标准温度，则因So＝0而有
其积分下限必须是零，积分时保持参量x不变。这样，熵的数值就完全被确定了。热力学第三定律本身不能用实验直接验证，其正确性是由它所得到的一切推论都与实验观测相合而得到了保证。下面用几个典型例子说明理论推论与实验观测值的符合情况：
①从第三定律出发并利用麦克斯韦关系推出温度趋于绝对零度时，物体的定压膨胀系数趋于零。图1是金的线胀系数α 随温度变化的曲线。可以看出，当T→0时，
与理论结果一致。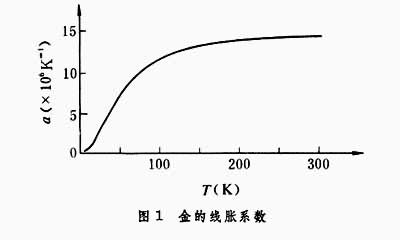
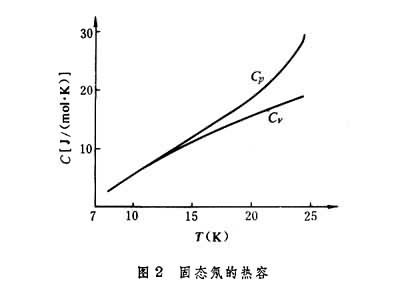
②理论推出
，图2为固态氖的（摩尔）热容随温度变化的实验曲线，它显示出低温时定压热容和定容热容趋于一致。③理论推出，固、液二相转变时的平衡压强随温度的变化，在T→0时，趋于零。图3表示出4He在低温下的熔解压力随温度变化的关系，由图可见，随T→0，斜率dP/dT趋于零。
第三定律在热力学中是根据实验事实总结出来的，但利用量子态的不连续概念，可以从量子统计理论导出它的结论。
参考书目
王竹溪著：《热力学》，高等教育出版社，北京，1955。
D. C. Kelly，Thermodynamics and Statistical Physics，Academic Press，New York and London， 1973.