水流能量方程(卷名：大气科学 海洋科学 水文科学)
energy equation of flow
描述水流各种形式的机械能相互转化和守恒的方程式。它是自然界普遍的能量转化和守恒定律在水流运动中的特殊表达形式。1738年首先由瑞士数学家D.伯努利提出，故又称伯努利方程。水流能量方程是研究水流运动基本方程之一。不同情况下的水流能量方程在形式上略有不同。
一维恒定总流的能量方程为：
若沿总流截取一段水流隔离体，则式中Z为隔离体上下断面上任一点从某一基准面算起的位置高度，代表单位水体从该基准面算起所具有的位置势能（位能），称为位置水头；p为同一点的动水压强，γ 为水的容重，
代表单位重量水体所具有的压强势能(压能)，称为压强水头；
反映了单位重量水体所具有的总势能，称为测压管水头;v为断面平均流速;α为考虑断面上流速分布不均而引进的动能修正系数，在一般的渐变水流中，α＝1.05～1.10，通常取α≈1.10;g为重力加度;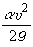
代表单位重体所具有的动能， 称为流速水头；
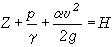代表单位重量水体所具有的总机械能，称为总水头;
是单位重量水体从断面1流到断面2(1～2)过程中，由于克服水流阻力作功而消耗的机械能，它转化成热能而散失，不能再恢复为其他形式的机械能，因此，习惯上称为水头损失。水流能量方程中各项的量纲均为长度，所以水流能量方程也可用几何线段来表示（见图）。
水流能量方程说明，水流在从一个断面流到另一个断面过程中，断面上各项能量（位能、压能、动能）在一定条件下可以相互转化，但前一个断面的单位总机械能（三项能量之和）应等于后一断面单位总机械能与两断面之间机械能损失之和。反映机械能转化又守恒的关系。
在应用水流能量方程时应注意到：①两断面间没有能量输入和输出，如动力机械对水流作功或水流对水力机械作功等；②所取断面一般宜在渐变流动中，但两断面间可以不是渐变流；③在计算的流段中有流量分出或汇入时（如引水或支流加入），应考虑满足上下断面和区间分出或汇入断面间全部水量的能量守恒；④应选取同一基准面，一般选在较低的位置上，以使Z≥0。压强水头是以当地大气压强等于零作为基准，用相对压强计算；⑤水流必须是恒定流，并符合连续原理。
在地下水运动中，由于流速很小，能量方程中的动能项可以不计，能量方程简化为
它表明地下水运动时克服阻力所消耗的能量完全由位能来补偿。对非恒定水流，能量方程中还必须考虑水流克服惯性所引起的能量损失。水流能量方程在研究河水运动、河口水流、地下水运动、河流泥沙运动中被广泛应用。