秦九韶(约1202～约1261)(卷名：数学)
中国南宋数学家。字道古，普州安岳（今四川省安岳县）人。活动在南宋末年，青少年饱经战争忧患，成年后被迫离开四川，在湖北、安微、江苏、浙江等地做官，晚年受贾似道打击，贬于梅州，“在梅治政不辍”，死于任所。秦九韶自称年轻时在杭州“访习于太史，又尝从隐君子受数学”。他知识渊博，当时人们称他“性极机巧，星象、音律、算术以至营造等事无不精究”。
秦九韶对数学的看法是矛盾的，他混淆了数学科学和术数的界限，把“通神明，顺性命”看成大者，把“经世务，类万物”看成小者，并进而认为河图、洛书揭开了数学的奥秘，说“数与道非二本”，表示要把他的数学成就“进之于道”。然而，数学研究的实践又使他承认他对通神明、顺性命的认识非常肤浅，承认“数术之传，以实为体”，从而把主要精力用于“经世务”，从社会实践和需要抽象数学问题。
秦九韶论述了数学在计算日月五星位置、改革历法、测量雨雪、度量田域、测高求远、军事部署、财政管理、建筑工程以及商业贸易等中的巨大作用，认为不进行计算会造成“财蠹力伤”的后果，而计算不准确，“差之毫厘，谬乃千百”，于私于公都没有好处。因此他注意搜求生产、生活、交换以及战争中的数学问题，“设为问答以拟于用”，终于在1247年写成杰作《数书九章》。
《数书九章》，南宋时称为《数学大略》或《数术大略》，明朝时又称为《数学九章》。全书共18卷，81题，分为九大类。第一，大衍类，集中阐述了他的重要成就──大衍求一术，即一次同余式组解法（见孙子剩余定理）。秦九韶指出“大衍之法不载九章”，历算家制定历法时虽然用到这种方法，但误以为是线性方程组问题。他总结了历算家计算上元积年的方法，在《孙子算经》“物不知数”题的基础上，系统地提出了一次同余式组解法。并针对不同的情况，提出了不同的程序。他还把这种理论用于解决商功、利息、粟米、建筑等问题。第二，天时类，是有关历法推算及降雨降雪量的测量。第三，田域类，是面积问题。第四，测望类，是勾股重差问题。第五，赋役类，是均输及租税问题。第六，钱谷类，是粮谷转运和仓库容积问题。第七，营建类，是建筑工程问题。第八，军旅类，是营盘布置及军需供应问题。第九，市易类，是交易及利息问题。后八类问题都是按应用分类，其中最重要的成就是正负开方术，今称秦九韶程序，即以增乘开方法为主导求高次方程正根的方法。他用这种方法解决了21个问题共26个方程，其中二次方程20个，三次方程1个，四次方程4个，还用勾股差率列出了一个十次方程。在这里，秦九韶把贾宪开创的增乘开方法发展到十分完备的地步。在开方中，他发展了刘徽开方不尽求微数的思想，在世界数学史上第一次用十进小数表示无理根的近似值。其次是在卷五“三斜求积”题中提出了已知三角形三边ɑ，b，с，求面积的公式
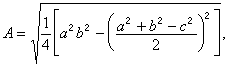这个公式与古希腊的海伦公式
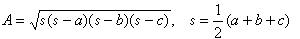是等价的。另外，他改进了线性方程组解法，普遍用互乘相消法代替“直除法”，并在互乘之前，先约去公因子，使运算更加简便。与以往的数学著作比较，《数书九章》中的问题更加复杂，如卷十三“计定筑城”题已知条件达88个，卷九“复邑修赋”题的答案有180个。因此，《数书九章》也更加翔实地反映了南宋的社会经济情况，保存了非常有价值的历史资料。
《数书九章》也有不容忽视的缺点。如第一题将大衍求一术附会《周易》“大衍之数五十，其用四十有九”，不足为训。还有一些问题，甚至某些不难的勾股测量问题，题设和演算都出现错误。
《数书九章》问世后，当时流传不广，明《永乐大典》钞录此书，称为《数学九章》。清四库馆本《数学九章》转录自《永乐大典》，并加校订。后李锐又略加校注。明万历年间赵琦美有另一钞本《数书九章》。清沈钦裴、宋景昌以赵本为主，参考各家校本，重加校订，1842年收入上海郁松年所刻《宜稼堂丛书》。此后，又有《古今算学丛书》本，商务印书馆《丛书集成》本均据此翻印，成为最流行的版本。