范畴(卷名：数学)
category
从数学的各个领域中概括出来的一种高度抽象的数学系统。数学的各个领域都有各自的研究对象。例如，集合论研究集合与映射；群论研究群与群同态；拓扑学研究拓扑空间与连续映射；等等。在20世纪中期，数学家们认为有必要将各个领域中的研究对象各自合在一起成为一个总体，使之各个总体都是一种数学系统。这就是范畴思想。于是，所有的集合与映射组成集合的范畴S；所有的群与群同态组成群的范畴G;所有的拓扑空间与连续映射组成拓扑空间的范畴T;等等。此外，在范畴与范畴之间往往存在着内在的联系与变换。例如，任一个群G都可以通过交换化手续而变成一个交换群(以C(G)表示G的换位子群，则G/C(G)是一个变换群)，因此交换化手续就把群范畴变成交换群的范畴AG。这种内在的联系与变换，提供了所谓函子的概念。
范畴与函子的理论是由美国数学家S.艾伦伯格与S.麦克莱恩于1945年正式提出的。这理论一经提出就受到普遍的重视而迅速发展，不断深入，且为数学家们引进到数学的许多分支中。例如，R.戈德门特于1958年引进到拓扑学中；C.埃雷斯曼于1958年引进到微分几何学中；A.格罗腾迪克、J.迪厄多内于1960年引进到代数几何中；等等。事实上，在数学的许多分支中都有范畴与函子理论的重要应用与反映。
定义和例子 范畴的定义是对集合范畴S、群范畴G、拓扑空间的范畴T 的一些共同性质的归纳。
一个范畴C，是由以下的三种成员组成的：
C1 一类对象A，B，C，…。
C2 对每两个对象(相同或相异)A与B，有一个集合C(A，B)与之对应，C(A，B)中元素σ称为态射(morphism)，A是σ的定义域，B是σ的变区。
C3 一种乘法，使得当σ∈C(A，B)，τ∈C(B，C)时，乘积τσ∈C(A，C)。它们都应该服从以下的三条公理：
A1 除非A＝A′而且B=B′，C(A，B)∩C(A′，B′)总是空集。
A2 在σ∈C(A，B)，τ∈C(B，C)，ρ ∈C(C，D)时，总有结合律(ρτ)σ =ρ(τσ)。
A3 对任何A，必有一个1A∈C(A，A)，称为恒等态射，使得对任何σ∈C(A，B)，恒有σ1A=σ=1Bσ。
对于σ∈C(A，B)，若有σ′∈C(B，A)，使σσ′=1A，而且σ′σ=1A，则σ称为一个同构态射，这时A与B称为同构的。同构显然是一种等价关系，所以，同构的对象称为本质相等的。
例如，在范畴 S中，对象类是所有的集合之类，而S(A，B)是由集合A到B的所有映射之集，在σ∈S(A，B)，τ∈S(B，C)，α∈A时，(τσ)(α)=τ(σ(α))∈C，即τσ∈S(A，C)。在范畴AG中，对象是交换群，AG(A，B)是由交换群A到B的所有群同态之集。再若以所有的自由交换群之类为对象类，以群同态为态射，则得自由交换群的范畴AFG。从这些例子看来，范畴中的态射可以是映射，甚至可以是同态（因而称之为态射）。但是，一般地，一个范畴的态射却可以根本不是映射。例如:①取N为自然数集。若α│b，则定义N(α，b)为一个单元集合，其惟一的元素是一个符号φ
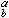，并令
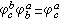;若α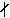
b，则N（α，b）为空集。于是，N是一个以所有的自然数为对象，以N(α，b)为态射集的范畴。②取R为全体实数的集合。在α≤b时，令R(α，b)是一个以符号Ψ
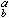为惟一元素的单元集合;否则让R(α，b)为空集。则全体实数连同所有的R(α，b)是一个范畴。③若范畴C只有一个对象M ，则C(M ，M )就是一个幺半群(即有单位元的半群)，而1M是这个幺半群的单位元。交换图 任意范畴 C中的每一个σ∈C(A，B)都可用一个箭头来表示成σ:A→B，或
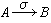，A是σ的源，B是σ的靶，用箭头的记号，所以态射又可称之为箭头。态射与态射之间的关系往往可以用交换图
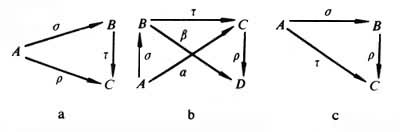来表示。例如，在已声明可交换的条件下依次表示ρ=τσ;ρα=ρ(τσ)=βσ=(ρτ)σ；与扽ρ，使ρσ＝τ。交换图中的虚箭头常用来代表未知的或待定的态射。泛性质 它是一种非常重要的范畴概念，常被用来提出或构造出许多新的概念。例如，设Г 是一个非空集合，对每一个λ∈Г 取一个集合Aλ，于是，由集合论，所有这些 Aλ 之积
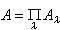也是一个集合，它是由所有如α＝{αλ|αλ∈Aλ，λ∈Г}这样的集合所组成的。但是这种积的定义却无法照样引用于一般的范畴，因为在一般的范畴中并不要求其对象是集合，更未要求有“α∈A”这样的概念。因此，若要想将积的概念引用于一般的范畴，则必须应用范畴的语言。首先注意到，若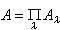则对每一个λ∈Г，都有∏λ：A→Aλ使当α={αλ}时
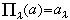而且对任何集合B与σλ：B→Aλ，必能找到惟一的ƒ：B→A，使对任何λ∈Г，恒有
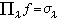，这只要让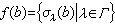
即可。这个性质可用来作为一般的范畴中一集对象的积的定义：范畴C中一集对象{Aλ｜λ∈Г}的积∏Aλ是一个对象A及一集态射 {∏λ∈C(A，Aλ)｜λ∈Г}，它对任何对象B及任何态射σλ：B→Aλ恒有惟一的ƒ:B→A使
，
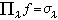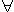λ∈Г，使有交换图(如图
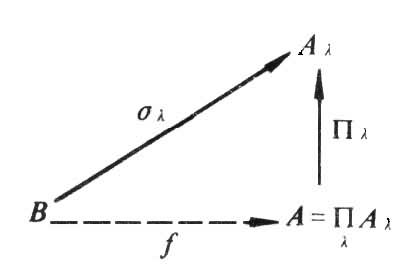)。 这里的"对任何态射σλ，恒有惟一的ƒ，使有交换图"一语，就是泛性质的意义。按照这个定义，在前面的例①的范畴N中，n个自然数α1，α2，…，αn的积(这里是指范畴N中这n个对象的积)是它们的最大公因数。在例②的范畴R中，实数集 {αλ}的积是这个集的下确界。
在任意的范畴 C 中，如果一集对象 {Aλ} 有积（A，
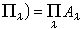那么它们只能有一个积（在同构的范围内），由泛性质所定义的任何概念只要存在，都具有唯一性。逆范畴与对偶原则 对于以A，B，C，…为对象的范畴C，可以作一个新的范畴C0，它仍以A，B，C，…为对象，但为了区别起见，在作为C0的对象时，A改写成A0，再取C0(A0，B0)＝C(B，A)，并当σ0∈C0(A0，B0)，τ0∈C0(B0，C0)时，定义τ0σ0=(στ)0，这样所作的范畴C0称为C 的逆范畴。实际上它们有相同的对象，相同的态射，只是把态射的源与靶恰好相互转换一下而已。
若S是一句对任何范畴都有意义的陈述语（例如，说明一个概念，提出一条命题，肯定一个规律，等等），把S引用到范畴C，得到S(C)，再引用到C0得到S(C0)，则在把 S(C0)中各态射的源与靶对调后，就变成（或翻译成）一句可引用于C 的陈述语 S0(C)。这个S0(C)就是S(C)的对偶陈述语。如果S(C)是一条命题，那么S0(C)是其对偶命题；如果S(C)是说明一个概念，那么S0(C)是说明其对偶概念;如果S(C)是一条对任何C都已证明了的定理，那么S0(C)是其对偶定理而且不需再证，这就是对偶原则。例如，在范畴C中，若σ1τ＝σ2τ时必有σ1＝σ2，则τ称为一个满态射；若τρ1＝τρ2时必有 ρ1＝ρ2，则τ称为一个单态射。于是，在C0中，τ0是满态射的条件为：当
时必有
，把这个条件翻译成C中的条件，就是τρ1=τρ2时必然ρ1=ρ2，这恰好是单态射的条件。因此，单态射和满态射是相互对偶的概念。在用一个交换图来表达一句陈述语S时，只要把这个交换图中所有的箭头都调转方向，并将“单”改成“满”，“满”改成“单”，这样所得的交换图就表达S的对偶陈述语S0。例如，将交换图中所有箭头都调转方向，就得到一集对象 {Aλ｜λ∈Г} 的上积
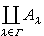的定义：一集对象{Aλ}的上积是一个对象C与一集态射ηλ:Aλ→C，使有泛性质：即，对任何τλ:Aλ→D，恒有惟一的g:C→D使gηλ=τλ，凬λ∈Г。不难证明，在范畴S中，一些集合Aλ(λ∈Г)的和集
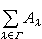（把Aλ都看成两两不相交的集合，再取其并集）就是诸Aλ的上积。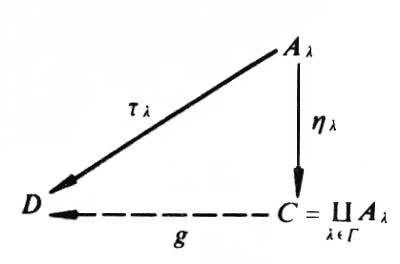
核与上核是另一对非常重要的对偶概念。在定义一个态射的核以前，先需定义零对象与零态射。若对于任何对象A与B集合C(A，0)与C(0，B)都是单元集合，则0称为范畴C中的零对象（因此用“0”这个记号）而C(A，0)与C(0，B)中的惟一元素分别记为
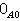与
， 把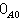
、
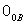以及它们的乘积
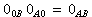都称为零态射，也用“0”这个记号来表示。例如在群范畴G中，零对象是只含一个元素的群，而当g与H是两个群时，0GH是由g 映射成H 的单位元的同态。用泛性质定义态射σ∈C(A，B)的核。设 η:C→A，使得：①ση=0，②对任何η′∈C(C′，A)，只要ση′=0，就必有惟一的ƒ∈C(C′，C)使ηƒ=η′，则(C，η)称为态射σ的核，记成Kerσ=(C，η)，有时可把C省去，得η=Kerσ，因给定了η，其源自然是确定的。这个泛性质可由图
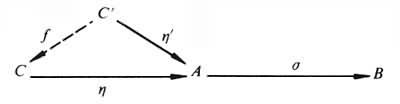表示。对偶地，态射σ∈C(A，B)的上核Cokσ是一个对象D及态射π:B→D，使得：①πσ=0，②对任何π′:B→D′，只要π′σ=0，必有惟一的g:D→D′，使gπ=π′，如图
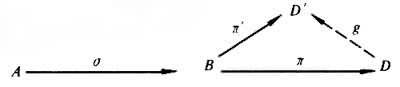。容易证明，若η=Kerσ，则η是单态射。其对偶定理是，若π＝Cokσ，则π是满态射。例如，在群范畴G 内，σ∈G(A， B)是由群A到B的一个群同态，其核C是同态σ的核，η是嵌入映射，若(D，π)=Cokσ，则D＝B/N，这里N是B中包含Im σ的最小的正规子群， 而π 是由B到 B/N的满同态(Im σ表σ的像)。
加法范畴与阿贝尔范畴 假定范畴C有零对象因而有零态射，如果：①任何有限个对象都有积；②每一个态射集C(A，B)都是交换群，并且当σ，τ∈C (A，B)，ƒ∈C(C，A)，g∈C(B，D)时，有分配律(σ+τ)ƒ=σƒ+τƒ，g(σ+τ)=gσ+gτ，那么C称为一个加法范畴。
若C是一个加法范畴，而且①每一个态射都有核与上核；②每一个单（满）态射都是其上核（核）的核（上核）；③每一个态射σ都可分解成一个单态射η与一个满态射π之积，σ=ηπ，则C称为一个阿贝尔范畴。
交换群的范畴Ag是一个阿贝尔范畴。如果A与B都是交换群，而 σ与 τ都是由A到B的群同态，那么在α∈A时，定义(σ+τ)(α)=σ(α)+τ(α)。逐条验证，即知Ag满足阿贝尔范畴的所有条件。自由交换群所组成的范畴是一个加法范畴，但不是阿贝尔范畴，因为可以找到单同态不是其上核的核。
函子 由范畴C到范畴C′的一个函子F:C→C′是一种双重意义的对应，一方面，它对C中的每一个对象A取C′中的一个对象F(A)与之对应，而另一方面，对于任何σ∈C(A，B)有一个F(σ)∈C′(F(A)，F(B))与之对应，使
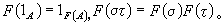从定义即可看出，函子事实上是范畴的同态。例如，取G为群范畴，Ag为交换群的范畴，F为交换化手续，则对任何群g，F(g)是一个交换群，同时，任何群同态σ：g1→g2 必将 G1的换位子群C (g1) 的元素变成 C (g2) 中的元素，所以，σ可引出g1/C(g1)到g2/C(g2)的一个群同态F(σ)。若C与C′都是加法范畴，而函子F:C→C′给出交换群C(A，B)到交换群C′(F(A)，F(B))的一个同态，则F 称为加法函子。
假定F与F′都是由C到C′的函子，若有一个规则t，使对C中任何对象A有一个态射tA∈C′(F(A)，F′(A))，对任何σ∈C(A，B)（图
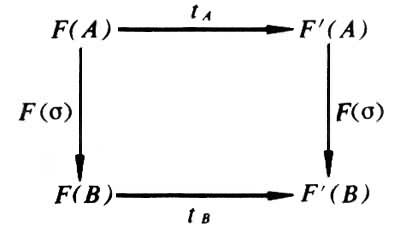），则t称为一个自然变换。自然变换把F 的性质变成F′的相应性质。特别，若对所有的A、tA都是同构，则F与F′称为自然等价。对于范畴C与C′，若有函子F:C→C′，与g:C′→D，使GF与 C的恒等函子（即让对象与态射都不变）自然等价，FG与C′的恒等函子自然等价，则C与C′是相互等价的范畴，等价的范畴有相同的范畴性质。
以上所述的函子严格地说，应该称为共变函子。由范畴C到范畴D的逆范畴D0的函子 F:C→D0，称为由C到D的逆变函子，在这样的函子中，若 σ∈C(A，B)，则F(σ)∈D(F(B)，F(A))，而且F(στ)=F(τ)F(σ)。举一个常见的例子，在范畴S中，固定一个集合C，对于任一集合A，定义F(A)=S(A，C)，任取σ∈S(A，B)，在ƒ∈S(B，C)时，定义F(σ)(ƒ)=ƒσ，如图
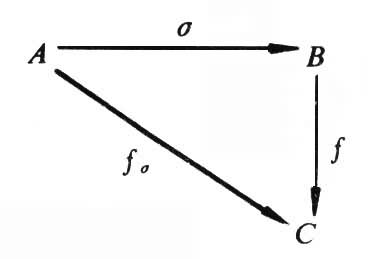，即F(σ)∈S(F(B)，F(A))，所以F是S到它自身的一个逆变函子。参考书目
B.Mitchell，Theory of categories，Academic Press，New York， 1965.