线性变换(卷名：数学)
linear transformation
同一域上两个向量空间之间的映射，是线性代数的一个主要研究对象。
设V和V′是域 K上的向量空间，L是从V到V′的映射，如果对于V中任意向量 u、v以及K中任意元素α、b，有L(αu+bv)=αL(u)+b)L(v)，那么L 称为V到V′的线性变换。例如，解析几何里的三维空间中任一向量(尣，y，z)在xy平面上的投影:L((尣，y，z))=(尣，y)，就是实数域R上三维向量空间R3到二维向量空间R2的一个线性变换。设尣是n维向量，M是m×n实矩阵，令L(尣)=M·尣，则L就是Rn到Rm的一个线性变换。
设L 是V 到V′的一个线性变换， B ={b)j|j=1，2，…，n}和 C ={сj|i=1，2，…，m}分别是 V 和V′的基，于是，V 中任一元素尣可表为
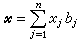，其中xj是域K的元素。由线性变换的定义可推得
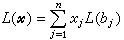。若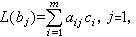
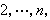式中αij是域 K 的元素，令M(L)=(αij)，尣写为列向量(x1，x2，…xn)T，则L(尣)＝M(L)·尣。此时M(L)称为L对(B，C)基的矩阵。当基取定之后，就在L与M(L)之间建立了一一对应关系，即V到V的一切线性变换与K上一切n×m 矩阵之间是一一对应的。线性变换保持子空间及其包含关系，即若S1、S2都是V的子空间，且有
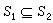时，则L(S1)、L(S2)必是V′的子空间，且有
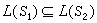。V′的零向量在V中的原像组成的集合，称为L的核，记作KerL，L(V)表示V在L作用下的像，则KerL和L(V)分别为V和V′的子空间，若以dim KerL 和dimL(V)分别表示子空间KerL 和L(V)的维数，则有dimKerL+dimL(V)=dimV。dim KerL称为L的亏，dimL(V)称为L的秩。从线性变换和矩阵的对应关系可知这两者是同一的，但是线性变换的矩阵与基有关，而线性变换却不受基的限制，所以线性变换使用起来要方便一些。例如，解齐次线性方程组：
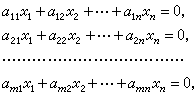就可看作求KerL的问题，这里L是矩阵(αij)所代表的线性变换。因此，当L的亏为0时方程组只有零解。在m<n时，由亏和秩的关系可知dimL(V)在V=V′时，若V 到V′的线性变换L是一个双射，则L 称为可逆变换或非奇异变换。从亏和秩的关系可知以下条件是等价的:①L是正则的;②M(L)是非奇异的;③L(V)=V；④KerV ={o}。V 的正则变换以映射的合成为运算构成一个群，称为V上的一般线性群，记作GL(V)。
在V和V′都是赋范线性空间时，V到V′的线性变换就称为线性算子。如果V′是一维实空间，那么就把线性算子称为线性泛函。对于线性算子L若存在常数M，使得‖L(尣)‖≤M·‖尣‖，对于V的一切x都成立，那么L称为有界的。对于线性算子来说，有界和一致连续是等价的。