非线性规划(卷名:数学)
nonlinear programming
目标函数是非线性函数或约束条件不全是线性等式(或不等式)的一类数学规划,即在问题
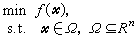 中,若ƒ(尣)为非线性的,或Ω不能用线性(不)等式表出,则此规划问题就称为非线性规划问题。由于问题的这种描述过于广泛,使得难于得到任何有深刻意义的结果。同时,对于某些特殊类型的Ω(例如Ω中点的坐标仅限于取某些整数值),需要特殊的方法去处理因而形成了一些独立的分支。非线性规划问题一般取如下的形式:
中,若ƒ(尣)为非线性的,或Ω不能用线性(不)等式表出,则此规划问题就称为非线性规划问题。由于问题的这种描述过于广泛,使得难于得到任何有深刻意义的结果。同时,对于某些特殊类型的Ω(例如Ω中点的坐标仅限于取某些整数值),需要特殊的方法去处理因而形成了一些独立的分支。非线性规划问题一般取如下的形式: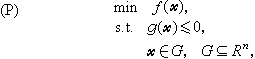 这里g(尣)=(g1(尣),g2(尣),…,gm(尣))为一给定的m 维向量实函数,g(尣)≤0表示它的所有分量皆不大于0,G为一给定的凸域,在多数情况下,
这里g(尣)=(g1(尣),g2(尣),…,gm(尣))为一给定的m 维向量实函数,g(尣)≤0表示它的所有分量皆不大于0,G为一给定的凸域,在多数情况下,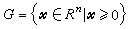 。Ω={尣∈Rn│g(尣)≤0,尣∈G}称为问题(P)的约束集,Ω中的点称为问题的可行解。若Ω=Rn,则此规划称为无约束规划,否则称为带约束规划。非线性规划主要包括以下四个方面的内容。
。Ω={尣∈Rn│g(尣)≤0,尣∈G}称为问题(P)的约束集,Ω中的点称为问题的可行解。若Ω=Rn,则此规划称为无约束规划,否则称为带约束规划。非线性规划主要包括以下四个方面的内容。算法 在ƒ(尣) 和Ω给定时,如何求出一个(或多个)点尣*∈Ω,使得ƒ(尣*)≤ƒ(尣)对所有尣∈Ω成立,是研究非线性规划的主要目的。因此,寻求能找出此尣*的算法便成为非线性规划研究的核心。目前尚未出现可以用来解决所有非线性规划问题的任何算法,算法的研究将是一个长期的课题。一般的算法都是迭代算法。除了某些特殊情况之外,求解的过程是一种无限过程,即逐渐逼近于所求的解。为了要判断一个算法所产生的点或所产生的极限点是否为所给问题的解,从而导致寻求解的充分必要条件。
充分必要条件 对一般的约束非线性规划问题:
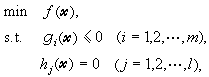 设函数ƒ、gi、hj都是一阶可微函数,
设函数ƒ、gi、hj都是一阶可微函数,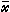 是一可行解。如果梯度
是一可行解。如果梯度 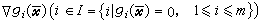 和墷hj(
和墷hj(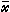 )(j=1,2,…,l)线性无关,那么
)(j=1,2,…,l)线性无关,那么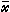 是一个局部极小点的必要条件为:存在u1,u2,…,um和v1,v2,…,vl,满足条件
是一个局部极小点的必要条件为:存在u1,u2,…,um和v1,v2,…,vl,满足条件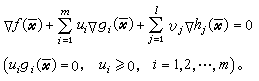 这一组条件称为库恩-塔克尔条件,又称为一阶必要条件。它是由H.W.库恩和A.W.塔克尔于1951年提出的。但是在凸性假设下,它又是充分条件。
这一组条件称为库恩-塔克尔条件,又称为一阶必要条件。它是由H.W.库恩和A.W.塔克尔于1951年提出的。但是在凸性假设下,它又是充分条件。库恩-塔克尔条件对于任意一个局部极小点并不一定成立。约束规格,是指约束条件在局部极小点处具有使库恩-塔克尔条件成立的性质。例如上述的“梯度墷gi(
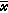 )和墷hj(
)和墷hj(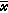 )是线性无关 (I∈I,j=1,2,…,l)”, 就是一种约束规格。此外,还有其他类型的约束规格。若gi,hi都是线性函数,则无需任何约束规格,此时库恩-塔克尔条件对于任意的局部极小点都成立。较之库恩-塔克尔条件为弱的必要条件是弗里茨·约翰条件,即对于局部极小点
)是线性无关 (I∈I,j=1,2,…,l)”, 就是一种约束规格。此外,还有其他类型的约束规格。若gi,hi都是线性函数,则无需任何约束规格,此时库恩-塔克尔条件对于任意的局部极小点都成立。较之库恩-塔克尔条件为弱的必要条件是弗里茨·约翰条件,即对于局部极小点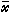 存在不全为零的数u0、ui和vj,满足条件
存在不全为零的数u0、ui和vj,满足条件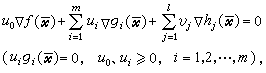 式中ƒ、gi、hj均为一阶可微函数。F.约翰在1948年提出这个条件,由于他没有考虑约束规格,因此他的条件中,主要参数u0可能为零而使此条件失效。
式中ƒ、gi、hj均为一阶可微函数。F.约翰在1948年提出这个条件,由于他没有考虑约束规格,因此他的条件中,主要参数u0可能为零而使此条件失效。对于不可微的凸规划,有推广的库恩-塔克尔条件。在推广库恩-塔克尔条件时需要引入次梯度的概念。设ƒ是Rn中的凸函数,若向量ξ满足
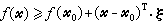 ,
,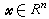 ,则向量ξ称为凸函数ƒ 在点尣0处的一个次梯度。函数ƒ在尣0处的次梯度不一定是惟一的。若凸函数ƒ在尣0处可微,它在尣0的次梯度即等于它在尣0的梯度墷ƒ(尣0)。对于不可微的凸规划
,则向量ξ称为凸函数ƒ 在点尣0处的一个次梯度。函数ƒ在尣0处的次梯度不一定是惟一的。若凸函数ƒ在尣0处可微,它在尣0的次梯度即等于它在尣0的梯度墷ƒ(尣0)。对于不可微的凸规划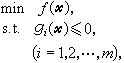 式中ƒ和gi都是凸函数。设gi满足斯雷特约束规格:存在一点尣0,使得gi(尣0)<0,i=1,2,…,m。则可行点
式中ƒ和gi都是凸函数。设gi满足斯雷特约束规格:存在一点尣0,使得gi(尣0)<0,i=1,2,…,m。则可行点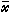 是凸规划的极小点的充分必要条件是存在数u1,u2,…,um 和ƒ在
是凸规划的极小点的充分必要条件是存在数u1,u2,…,um 和ƒ在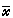 处的次梯度ξ、gi在
处的次梯度ξ、gi在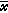 处的次梯度ξi,i=1,2,…,m,满足条件
处的次梯度ξi,i=1,2,…,m,满足条件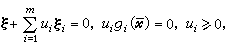 i=1,2,…,m。
i=1,2,…,m。对偶问题 是指根据 (P)中的数据建立起来的一个与所给的问题(P)伴随的问题(P*)。 (P)与(P*)之间有如下的关系:
①若(P)是求目标函数ƒ(尣)的极小(大)值,则(P*)是求某一目标函数 l(у)的极大(小)值;②对于(P)与(P*)的可行解尣与у,常有ƒ(尣)≥l(у)(ƒ(尣)≤l(у));③(P)与(P*)在 x*与у*取最优值的充分必要条件是l(у*)=ƒ(尣*)。
对于所给定的(P),能满足上述三种性质的(P*)一般并不是惟一的。因此就存在构造(P*)的不同途径。目前研究对偶性主要有两条途径。
其一是利用拉格朗日乘子。例如线性规划(P):
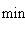
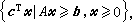 已知其对偶问题(P*)是
已知其对偶问题(P*)是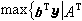
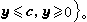 记
记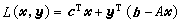 是(P)的拉格朗日函数,则(P,P*)显然分别等价于以下两个极值问题
是(P)的拉格朗日函数,则(P,P*)显然分别等价于以下两个极值问题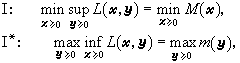 这里,I(I*)中之min(max)只限于就
这里,I(I*)中之min(max)只限于就 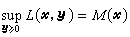
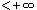 (或
(或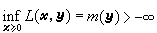 )之尣(或у)来取。
)之尣(或у)来取。一般,令
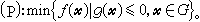 作(P)的拉格朗日函数
作(P)的拉格朗日函数 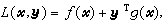 则(P)即等价于
则(P)即等价于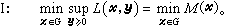 其对偶问题为
其对偶问题为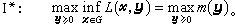
更一般言之,设φ(尣,у)为定义在X×Y上的实函数,于此,X吇Rn,Y吇Rm。作
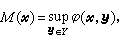
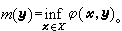 记
记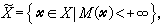
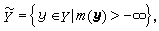 则(P):
则(P):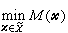 与
与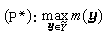 分别称为原规划和对偶规划。不难证明,若X与Y皆为紧致凸集,φ(尣,у)在X×Y上为连续,且对于固定的у∈Y(尣∈X),φ(尣,y)为X(Y)上的凸(凹)函数,则上述性质①、②、③皆成立。
分别称为原规划和对偶规划。不难证明,若X与Y皆为紧致凸集,φ(尣,у)在X×Y上为连续,且对于固定的у∈Y(尣∈X),φ(尣,y)为X(Y)上的凸(凹)函数,则上述性质①、②、③皆成立。其二是利用共轭函数。若ƒ(或l)为定义在凸集C吇Rn(D吇Rn)上之凸(凹)函数,则称
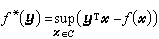
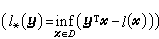 为ƒ(或l)的凸(凹)共轭函数。记
为ƒ(或l)的凸(凹)共轭函数。记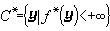 ,
,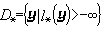 ,则(P):
,则(P):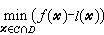 与
与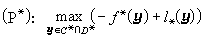 即互为对偶。实际上,性质①与②是显然成立的。 至于③,则有下面定理:设C与D有公共内点,且
即互为对偶。实际上,性质①与②是显然成立的。 至于③,则有下面定理:设C与D有公共内点,且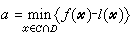 为有限,则存在
为有限,则存在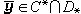 ,使得
,使得 。
。上述两条途径皆得到了深入的发展,特别是R.T.洛卡费勒基于增广拉格朗日函数发展了一般的对偶理论。
研究对偶理论的目的主要有三:一是某些实际问题,特别是某些经济问题,其中所出现的某些现象用对偶理论容易得到解释;二是可以利用它来帮助求解原问题;三是判定原问题是否有解。例如,有时(P*)比(P)容易得到解决,利用性质③即可得出ƒ(尣)的极值;性质②有助于求ƒ(尣)的下界。这一点在分枝定界法中常用到。对偶问题的出现是相当普遍的。数学规划中的许多分支,例如整数规划,参数规划、模糊规划等皆有类似的问题和不同深度的处理。
稳定性 一个数学规划问题
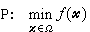 已经给定,意即ƒ(尣)和Ω已经用某种关系和数据具体表出。所谓稳定性,是指当这些数据作微小变动时问题的解所受到的影响的程度。关于这类问题的研究也称为灵敏度研究。参数规划就是这类问题的一个扩充。
已经给定,意即ƒ(尣)和Ω已经用某种关系和数据具体表出。所谓稳定性,是指当这些数据作微小变动时问题的解所受到的影响的程度。关于这类问题的研究也称为灵敏度研究。参数规划就是这类问题的一个扩充。形如
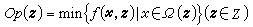 的规划称为参数规划,式中的
的规划称为参数规划,式中的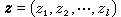 是参数。对于一个给定的z∈Z,就得出一个具体的数学规划。参数规划的研究目的之一,就是要在Z中求出一个子集 Z′,使得Op(z)对所有的z∈Z′具有某种给定的性质。例如要在Z中求出使得Ω(z)非空的z所成之集,使得Op(z)为可解的z所成之集(即存在尣*∈Ω(z),使得ƒ(尣*,z)=Op(z)),以及使得Op(z)的解集是具有某种共同给定的结构的z所成之集,等等。求解参数规划Op(z)(z∈Z)是指寻求Z 中的一个子集,对于其中的z,Op(z)成为一个关于某种性质是不变的数学规划问题。参数规划的研究内容主要包括以下几个方面:解的稳定性问题;解对于初始数据的依存关系;初始数据依某种方式具有不确定性的问题(例如,某些量只知其属于某一区间、某些量是随机变量,等等);在一类数学规划问题中,寻求其中容易解决者;寻求可以用来处理和衡量其他最优化问题的辅助手段;研究某些问题类的一般性质,并发展一般性的方法,等等。
是参数。对于一个给定的z∈Z,就得出一个具体的数学规划。参数规划的研究目的之一,就是要在Z中求出一个子集 Z′,使得Op(z)对所有的z∈Z′具有某种给定的性质。例如要在Z中求出使得Ω(z)非空的z所成之集,使得Op(z)为可解的z所成之集(即存在尣*∈Ω(z),使得ƒ(尣*,z)=Op(z)),以及使得Op(z)的解集是具有某种共同给定的结构的z所成之集,等等。求解参数规划Op(z)(z∈Z)是指寻求Z 中的一个子集,对于其中的z,Op(z)成为一个关于某种性质是不变的数学规划问题。参数规划的研究内容主要包括以下几个方面:解的稳定性问题;解对于初始数据的依存关系;初始数据依某种方式具有不确定性的问题(例如,某些量只知其属于某一区间、某些量是随机变量,等等);在一类数学规划问题中,寻求其中容易解决者;寻求可以用来处理和衡量其他最优化问题的辅助手段;研究某些问题类的一般性质,并发展一般性的方法,等等。非线性规划是极值理论的一部分。早在17世纪P.de费马提出如下的问题:对于平面上给定的三点,要作一点使其与这三点的距离之和为最小。它的对偶问题:过所给三点作一最大的等边三角形,也早在18世纪初即已提出,并证明了这两问题之间存在对偶关系。
对具有等式约束的非线性规划的解应满足的必要条件的研究,可上溯到L.欧拉和J.-L.拉格朗日时代。W.卡鲁什在1939年开始了对具有不等式约束的非线性规划的类似问题的研究,但由于他的工作没有正式发表,同时由于当时计算机尚未出现,数学规划不能在生产实际中产生影响,这项工作便湮没无闻。非线性规划的发展是由于线性规划的出现而引起的。1951年H.W.库恩和A.W.塔克尔的研究工作,虽是重复了W.卡鲁什的结果,但可以看作是非线性规划理论工作的先驱。这组条件更合适的名称应该是卡鲁什-库恩-塔克尔条件。
参考书目
M.阿弗里耳著,李元熹等译:《非线性规划──分析与方法》,上海科学技术出版社,上海,1979。(M.Avriel,Nonlinear Programming-Analysis and Methods, Prentice-Hall,Englewood Ciffs,New Jersey,1976.)