边界层(卷名：力学)
boundary layer
如果粘性很小的流体（如水、空气等）在大雷诺数时与物体接触并有相对运动，则靠近物面的薄流体层因受粘性剪应力而使速度减小；紧贴物面的流体粘附在物面上，与物面的相对速度等于零；由物面向上，各层的速度逐渐增加，直到与自由流速相等。L.普朗特把从物面向上的这一流体减速薄层叫作边界层。图1是水由左向右沿静止薄平板流动时，在水面上洒金属粉后，用闪光灯拍下的照片。从停滞在平板面上的粉末中，可以清楚地看出板面附近的边界层。图2表示在边界层内速度由板上的零值向上渐增的速度u(x，y)分布图、边界层的厚度δ和它在x方向变化的情况，图中U为自由流速。
边界层呈层流流动的，叫层流边界层；呈湍(紊)流流动的，叫湍（紊）流边界层。
19世纪末古典流体力学理论由于与实验水力学分开，单纯搞数学解析，因而得出绕物体流动没有阻力的不符合实际情况的结果，这就是达朗伯佯谬。1904年普朗特从实际流动出发，通过实验观察，提出了边界层理论，把靠近物面的边界层按粘性流动计算，而把边界层外的流动仍按理想流体动力学计算，从而简化了纳维－斯托克斯方程，得出了阻力公式，部分地解决了达朗伯佯谬问题。边界层理论把流体力学理论与实验结合起来，给现代流体力学发展创出了新路。它对航空工程，水利工程，流体机械如涡轮、压缩机、泵和螺旋桨等的效率提高都有实用价值，因而几十年来边界层的实验和理论发展迅速。特别是近二十年来随着电子计算机的发展和测试技术的现代化，在理论和实验方面不断深入，尤其在湍流边界层、高速边界层、温度边界层、扩散边界层等各方面的研究都取得了进展（见化学反应边界层，边界层传热传质，激波与边界层相互干扰，烧蚀）。但在湍流结构等基本理论方面，还有待进一步研究。随着实验技术和电子计算机的发展，简单的边界层理论已不能满足需要，“多层边界层”近似理论正在研讨中。
下面只介绍低速（不可压缩流体流动）边界层理论。
边界层厚度 指在边界层内由物面(速度为零)垂直向上到与外界局部自由流速U相等的流线间的距离。由图2中的速度分布曲线可以看出，在边界层上边界附近的速度值是渐增的，所以很难精确地定出边界层厚度。一般把从物面起，到速度为0.995U处的厚度 δ定为边界层厚度。边界层厚度与流动的雷诺数、自由流的状态、物面粗糙度、物面形状和延展范围都有关系。沿物体边界层的厚度是由薄逐渐变厚的。当空气流的雷诺数为Rex＝106时，在距前缘1米处，平板上层流边界层的厚度为3.5毫米。在平滑平板上，层流边界层的厚度
(Rex=Ux/v，这里v为流体运动粘性系数)；写成等式时的常数值随所选取边界层厚度处的速度百分比（如选0.90，0.99或0.995）而异，一般为3.46到5.64。平滑平板上湍流边界层的厚度
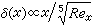，其比例常数约为0.37。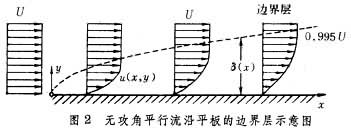
可以看出，由于测定边界层厚度有任意性，用它来计算摩擦阻力太粗糙，因而在实际应用中，又定义出其他的厚度。例如在低速时用位移厚度δ1（或δ*）、动量（损失）厚度 δ2（或θ），此外还有一个无量纲厚度比叫形状因子。
位移厚度 由于流体粘性阻滞而形成的边界层把层外主流从壁面向外推移的距离(图3)，
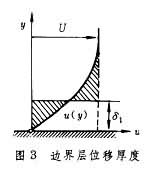可按定义由下式求出：
或
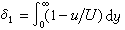。平行流流过平板时，层流边界层的 δ1≈δ/3，湍流边界层的δ1≈δ/8。动量（损失）厚度 因粘性阻滞，在边界层内所损失的动量，相当于按层外主流速度U计算时，这个动量所占的厚度，即
或
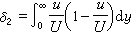。平行流流过平板时，层流边界层的δ2＝0.13δ，湍流边界层的δ2＝7δ/72＝0.097δ，故δ1＞δ2。形状因子 上面两个厚度比所组成的无量纲参数，通常表为：
δ1/δ2=H12（在低速时也写为H）。因δ1＞δ2，故H＞1。在层流边界层中，H的值由驻点附近的2.0到分离点的3.5。在湍流边界层中，它的值不定，大约为1.2～2.5。
边界层方程 边界层中流体运动所遵循的物理规律的数学表达式，包括边界层微分方程和分界层动量积分方程。
边界层微分方程 由于y与边界层厚度δ《x（物面方向长度）是同一量级，同时又
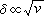，普朗特于1904年从纳维－斯托克斯方程出发把方程中各项的数量级写出并互相比较，最后将量级为δ2以上的项略去，得到边界层方程。例如，二维不可压缩流的层流边界层方程组可写为：运动方程
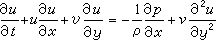，连续性方程
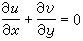，边界条件 y＝0，u＝v＝0；y＝∞，u＝U(x，t)，式中u、v为x、y方向的速度分量；p为压力;ρ为流体密度。原来y方向的动量方程简化成
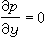，它表示在边界层内沿垂直于壁面方向的压力保持常值，即壁面上某点的压力p等于无粘性外流在此点计算出的p值，因此在边界层流动计算中，p被认为是已知的物理量。如果物面是曲面，可以选取曲面坐标系，沿物面方向为x，垂直于物面方向为y。同样得出
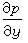在y方向的增长也是δ2的量级，可以忽略。关于湍流边界层方程，由于流动随时间、空间而变更，情况非常复杂，因而尚未通过实验弄清湍流的物理机理，得出公认的模型。所以多年来，人们针对不同情况提出了各种半经验理论和假设求平均流解。
在湍流边界的一般情形中，流体微团的瞬时速度可表为平均速度与脉动速度之和 (如x方向u=ū+u′等)。由于脉动速度间的动量交换而引起的湍流边界层中的附加湍流应力（也叫雷诺应力）是：
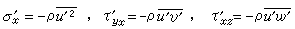等。它是一个张量。在二维情形中，雷诺应力τt可写成（见湍流理论）：
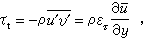式中ετ 称为涡粘性系数，上面的横线表示平均值。二维不可压缩湍流边界层的微分方程组为：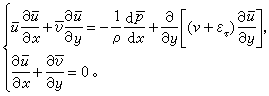
边界层动量积分方程 为T.von卡门于 1921年所提出，又称卡门积分关系式，是工程上常用的近似法，对定常、二维不可压缩层流和湍流（采用平均速度分量）边界层都能用。这个方程是在边界层内取一个控制微元，用动量定理使在 x方向的总动量增加率等于单位时间内流出动量与流进动量之差得出的。因为求动量是从壁面y=0到y=δ求积计算的，所以得出的是平均值，即是近似法。此积分关系式为：
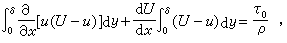式中τ0为物面上的剪应力。用位移厚度δ1和动量厚度δ2代入，可写成：
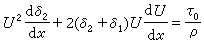或
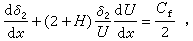式中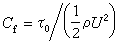
为摩擦系数。层流边界层 流体绕物体流动时，在物体的前端或上游部分的边界层，一般是层流边界层。在图2中沿平板前端的就是层流边界层的速度分布情况。沿曲面的层流边界层，由于外流速度有变化，与平板有所不同，但速度分布大致类似。紧贴物面的速度梯度较大，因而剪应力也较大。物面上的剪应力为：
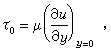式中μ 为流体动力粘性系数。算出了τ0，就可求出物面的摩擦阻力系数和摩擦阻力。但这些计算只能用于分离点以前。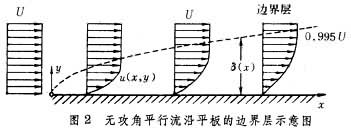
层流边界层的微分方程 比纳维－斯托克斯方程简单，但仍是非线性的偏微分方程。二维层流边界层方程的早期解法是找出无量纲的组合自变数，代入式内把方程变为常微分方程，再用级数法求出摩阻系数，或直接找它的数值解。这种方法叫“相似解”。“相似解”对绕平板流、绕楔形体流、收缩管道流、绕圆柱体对称流等都可用。由于近年来电子计算机的发展，已能用有限差分方法或有限元法直接求非线性偏微分方程的数值解。
层流边界层的动量积分 它比偏微分方程的数值解法简便得多，但不能提供边界层内详细的流动特性变化(如速度分布等)。因此若只要求边界层特征物理量（如位移厚度、壁面剪应力等）沿物面的变化情况，它是一种实用的工程方法。对一些复杂的流动问题，如粘性流动和非粘性流动的相互作用问题，还常常使用它来计算边界层的特性。
三维层流边界层的计算 如果是旋转对称体的绕流，可以通过转换式［如曼格勒 (Mangler)转换式］化成二维形式，就可利用现有的二维解。绕任意物体的三维计算，要比二维复杂得多，因此只能依靠数值求解的办法。
层流边界层的过渡和稳定性 自从O.雷诺对圆管流动的实验证明管内流动先是层流然后过渡到湍流后，他用一无量纲比值（即雷诺数）作为流动参数。对于每一种特定形状都有一个临界雷诺数，例如圆管流动的临界雷诺数为2000，超过这个值，层流就过渡到湍流（见层流）。在边界层内存在着类似的临界雷诺数概念，不过边界层的雷诺数通常写作Re=Uδ*/v。 临界雷诺数Recr可以通过实验得出。
层流向湍流过渡除与雷诺数关系最大外，还受其他许多参量的影响，例如外流的湍流度、逆压梯度、流体吹入、流过凹面上的离心力、非均匀流中的浮力、物面粗糙度、流体与物面的热交换等，都会增加不稳定因素，容易引起层流边界层的过渡。
层流边界层稳定性理论 在理论方面，常用小扰动稳定理论，即假设层流流动是由平均流动（可看作定常流动）加上小扰动正弦流动合成的，如果小扰动随时间的增加而增大，则是不稳定的，有可能过渡成湍流。通常所谓奥尔－索末菲方程就是小扰动理论的方程（见流体运动稳定性）。
讨论平行流边界层稳定性时，常用托尔明－施利希廷稳定性理论。它的基本思想是：层流边界层流过物面时，总要受到一些小的扰动(如尖端、粗糙板面等)，因而在层流边界层中，包含有许多振幅非常小的速度脉动，其频率范围很广。在某种情况下，若某一频率的脉动得到加强，而其他频率减弱，则前者在此频率下迅速增大振幅(在边界层内的这一波动叫作托尔明－施利希廷波)，使层流不稳定，导致形成湍流。反之，如果脉动的所有频率的振幅都减弱，则层流稳定。
层流边界层向湍流边界层的过渡 层流的稳定性理论并不能说明由层流向湍流过渡的全部物理现象。过渡是一个非常复杂的流动过程，直到目前为止，人们对它还没有很清楚的了解。从绕平板这样一个简单流动来看，若外流湍流度低，流过平滑平板时，层流边界层向湍流边界层过渡大致经过以下几个阶段(图4)：①靠近平板前端是稳定的层流边界层；②过临界雷诺数后，有不稳定的二维托尔明－施利希廷波；③不稳定的层流三维波继续发展，并形成小涡；④在很强的局部剪应力处，涡旋破裂，产生三维湍流脉动；⑤在湍流速度脉动很大的地方，产生许多湍流斑点；⑥许多湍流斑点联合在一起，发展成为完全发展了的湍流边界层。
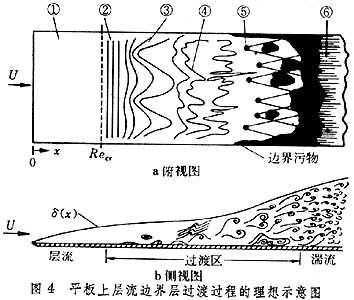
在大多数情况下，由湍流斑点发展成为完全湍流时，同时形成许多分离气泡。在上述过程中，目前只能对①、②、③进行理论分析，其他各过程还有待于今后进一步探索。
沿曲面有离心力的流动的不稳定性，与上述的不同。例如在两个能作同心旋转的内、外圆筒间的层流流动，当内筒旋转外筒不动时产生泰勒涡(见流体运动稳定性)，层流不稳定；而外筒旋转内筒不动时，层流稳定;两筒作相反方向旋转时又不稳定。又如沿凹面的层流流动，产生垂直于流向的格特勒涡，也引起不稳定。
当层流边界层过渡到湍流边界层后，边界层厚度 δ增大(图4)，同时阻力也增大。仍以平行流流过平板为例，阻力系数Cf与雷诺数Re两者的关系如图5（用双对数坐标）所示。
湍流边界层 在自然界和工程中，运动物体（如飞机、叶栅等）表面上的流动大部分是湍流边界层。由于湍流是有涡流动，有随机的脉动，流动随空间和时间都在变化，所以湍流边界层的内部结构比层流边界层复杂得多。由于湍流内有垂直于流向的动量交换，它在与壁面垂直截面上的速度分布与层流边界层的不同，下端丰满一些（图6）。
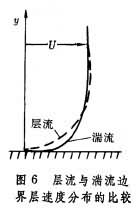
由实验数据，可把湍流边界层近似地看作由内区和外区组成。这样的分法是因为靠近壁面的粘性剪应力与压力梯度在这两个区内是截然不同的。内区包括贴近壁面的粘性底层，其中剪应力最大，由许多小旋涡组成；向上是缓冲层，再向上直到边界层外区是大尺寸旋涡组成的动量交换较大的湍流层。外区是从这个湍流层一直到速度与外流极相近的地方。总的说，内区占边界层全层的20％。
湍流边界层理论 从湍流边界层的研究历史来看，存在着两种理论，它们分别发展又相互关联。一种是统计理论，另一种是半经验理论。
① 在统计理论中，把流体看做连续介质，把流速、压力等的脉动值看做连续的随机函数，通过各脉动值的相关函数和谱函数来描述湍流流动。按统计平均法，从中找出脉动结构，把各种平均值代入纳维－斯托克斯方程及其他方程，得出所谓雷诺方程。但统计理论目前主要用于研究均匀各向同性湍流，对湍流边界层流动并不适合。
② 在另一种半经验理论中因为湍流边界层方程的数目少于未知量的数目，方程组是不封闭的，因而需要补充一些关系式，由此而产生的一些不严谨的近似理论为半经验理论。这些理论虽无严格的依据，但对解决工程上的许多问题很有用处。又因为其中有些系数是从实验中求出的，所以用这些半经验理论算出的结果，常与实验较吻合，但它们的适用范围有局限性。常用的半经验理论有：J.V.布森涅斯克于1877年提出的，用涡粘性系数计算雷诺应力的公式；普朗特的混合长理论（动量传递理论）；G.I.泰勒的涡旋传递理论；卡门的相似理论等。这些半经验理论的缺点是对湍流的内部结构都没有做分析，使用范围有限。
湍流边界层实验 对边界层的研究，实验是很重要的手段，尤其是湍流边界层测量，许多国家都成立了小组在不断地进行研究。一般实验是在水槽或风洞内进行的。所用的流场显示法有氢气泡法、烟迹法，涂在物面上的油流法等。测量方法近代多用热线、热膜和激光测速、激光全息摄影等（见湍流实验）。
边界层分离 流体流过曲面时，它的速度和压力都有变化。当流速减少时，压力必定增加。由于在边界层内的流体微团有动量损失，如遇到下游压力增加（即有逆压梯度）时，则动量再减少，直到流体微团不能再在物面上前进时就会从物面分离。这一现象叫做边界层分离(图7)。
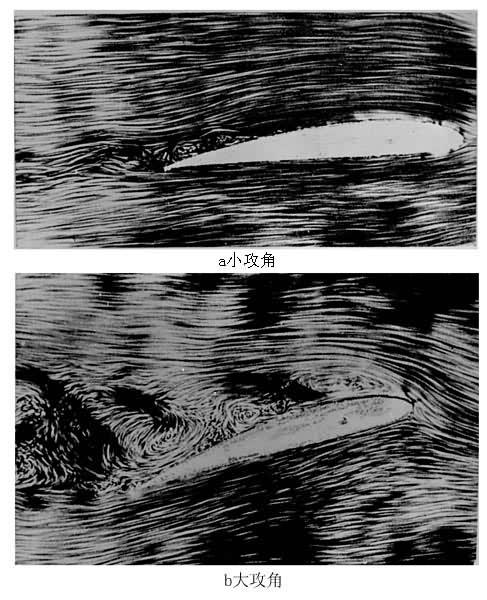气流开始离开物面的点称为分离点，它的位置是由物面处的
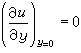来确定的，即该点在物面处的法向速度梯度为零。图8表示出平行流流过对称翼剖面的二维流动，在翼剖面后部有逆压梯度处边界层分离的情况，以及在分离点S附近的速度分布。注意在分离点处的速度分布曲线上有拐点，分离区内沿物面有反向（向前）的流动，产生涡旋，并形成物体后面的尾涡。机翼上边界层分离，使机翼的举力受到限制，并增加阻力。大攻角翼上分离会造成飞机的失速；涡轮泵、压气机、螺旋桨等的桨叶上的气流分离使机械效率降低，并能腐蚀壁面。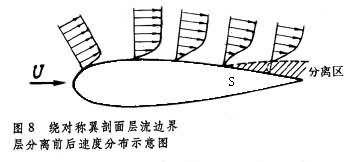
二维绕物体边界层分离有两种情况：一种是从分离点后，主流离开物面，并在下游形成较大的旋涡区。这种分离在一般攻角时，常发生在机翼（举例说）的后部（图7和图8）；另一种是从分离点S后，主流先离开物面，然后又在A点附着在物面上，形成气泡──局部回流区（图9）。
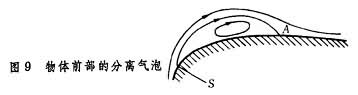分离气泡多是先层流分离，中间变为湍流，底层得到动能，再附着物面。在厚机翼时，分离常发生于机翼后部；在薄机翼时，则常在前缘附近产生气泡分离。三维边界层分离较复杂，甚至如何定义分离点，尚没有一致的看法。湍流边界层分离与层流边界层分离相同，但因湍流内部有上下的动量交换，对同一外形物体，湍流边界层的分离点比层流边界层靠后。在特定情况下，人们可以人为地固定分离点，利用气流分离后形成的涡旋对物体的作用，产生有利的效果。例如目前航空上采用边条小翼，就是利用它的前缘分离涡，以增加小展弦比的基本翼上的非线性举力。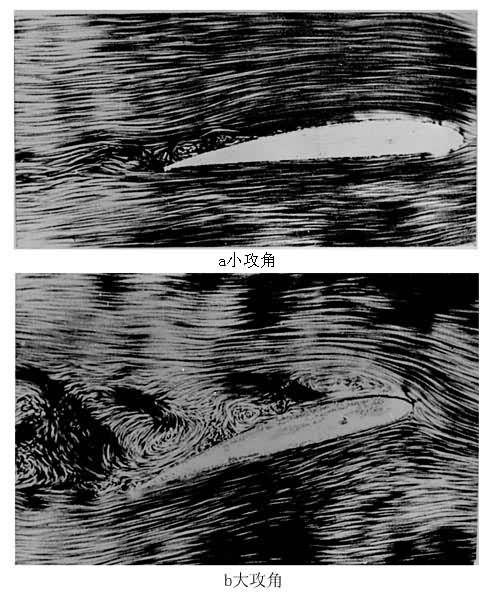
在实验方面，测分离点位置可用模型表面的油流法、丝线法和用普雷斯顿管等。
近年来各国对分离流尤其是对二维非定常流和三维定常流中边界层分离的起始及分离点、线附近流动问题的研究愈益重视，已有一些近似理论如三层结构等，也试提出二维、三维流动的分离判据，研究正在不断深入中。
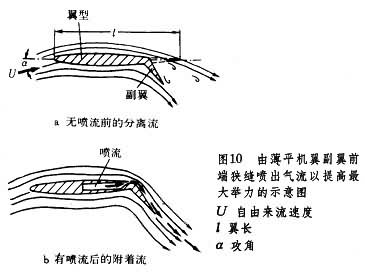
边界层控制 在应用上（例如对航空飞行器来说），层流边界层的过渡和分离，使机翼等阻力增加和(或)举力减少（甚至失速）；因此人们很早就设法使机翼表面光滑，并设计“层流翼剖面”，以维持层流边界层。但这种控制是有限的，所以人们后来采用了许多人工控制边界层的方法，以达到影响边界层结构，从而避免边界层内气流分离，和减少阻力增加举力的目的。实验和理论得出如下的使流体局部加速的几种有效方法：①使部分物面移动；②通过物面上的喷孔(狭缝)吹出流体，以增加表面滞流的能量（图10）；③通过物面上的狭缝，吸走滞流，使边界层变薄，以抑制分离；④用不同气体喷射，加速滞流；⑤变更机翼形状。
参考书目
H.Schlichting， Boundary Layer Theory，McGraw-Hill，New York，1979.
T.Cebeci and A.M.C.Smith，Analysis of TurbulentBoundary Layers，Academic Press，New York，1974.
F.M.怀特著，魏中磊、甄思淼译：《粘性流体动力学》，机械工业出版社，北京，1982。（F.M.White，Viscous Fluid Flow，McGraw-Hill，New York，1974.）
G.V.Lachmann，Boundary Layer and Flow Control，Perga mon Press，Oxford，1961.
P.Bradshaw， An Introduction to Turbulence and Its Measurement，Pergamon Press，Oxford，1971.