卡姆定理(卷名:自动控制与系统工程)
KAM theorem
关于哈密顿力学系统运动稳定性的一种论断,它反映“弱”不可积(或接近可积)系统的运动规律。卡姆定理是牛顿力学在20世纪的重大进展。这一定理于50年代中期至60年代初期由A.H.柯尔莫戈罗夫、В.И.阿诺德以及J.莫泽先后提出并分别予以证明,KAM即为三人姓氏的首字母。
人们对力学系统所关心的问题之一,是运动过程的长期行为和它最终会达到的状态。动力系统的长时间行为可能有多种形式:平衡或不动点,周期振动,准周期运动,混沌。它们都是定常态。牛顿力学的确定论观点曾因它解决太阳系行星运行问题的成功而在很长时期占统治地位。P.S.拉普拉斯曾宣称,只要给定初始条件就可以预言太阳系的整个未来。但是,力学中的三体问题和重刚体绕固定点的运动问题成为困扰人们近一个世纪的难题。数学家于19世纪认识到 N体问题属于不可积分的难题,只能寻求级数解。换言之,这类系统无法根据初始条件求出描述系统未来确定性行为的精确解。随之,H.庞加莱也清楚地认识到力学系统一般说来不可积分,可积分系统只是极少的特例,并指出共振项可能影响级数的收敛性。对于不可积系统的运动图像,卡姆定理回答了“弱”不可积系统的问题。假定这种系统的哈密顿量可以分为两部分。
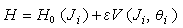 其中H0是可积的,因而只依赖于作用量Ji;V是使H变得不可积的扰动,自然含有角度变量θi。只要参数ε 很小,导致不可积的附加项就很小。卡姆定理指出:在扰动(或者说非线性)较小、V足够光滑、离开共振条件一定距离等三个条件下,对于绝大多数初始条件,弱不可积系统的运动图像与可积系统基本相同。可积系统的运动限制在由N个运动不变量决定的N维环面上,弱不可积系统的绝大多数轨道也限制在稍有畸变的N维环面上。这些环面称为不变环面或卡姆环面。确切些说,相空间分成大小两组体积非零的区域。在大区域中仍然保持着与可积系统类似的环面结构;初始条件如果落入小区域中,运动轨道就会相当不规则地迷走,运动轨道呈现不稳定性。这些小的不稳定区的体积随着ε 趋于零而消失,但只要ε 不为零,它们的体积就是有限的。这说明只有低阶(看来小于4阶)共振才有危险性,高阶共振不影响微扰级数的收敛性。低阶共振的区域在相空间中是彼此隔开的,只有参数ε足够大时,它们才会互相重叠,导致混沌运动。进一步的研究发现无论破坏任何一个卡姆条件,运动图像都会变得更为混沌。轨道的不稳定性是力学系统运动中出现随机性、不可预言性和混沌的原因。卡姆定理通过对弱不可积系统运动稳定性条件的证明,说明了三维以上非线性系统的运动轨道出现混沌现象具有普遍性。这对于突破牛顿力学决定论的思想框架具有重要意义,也丰富了系统学的内容。
其中H0是可积的,因而只依赖于作用量Ji;V是使H变得不可积的扰动,自然含有角度变量θi。只要参数ε 很小,导致不可积的附加项就很小。卡姆定理指出:在扰动(或者说非线性)较小、V足够光滑、离开共振条件一定距离等三个条件下,对于绝大多数初始条件,弱不可积系统的运动图像与可积系统基本相同。可积系统的运动限制在由N个运动不变量决定的N维环面上,弱不可积系统的绝大多数轨道也限制在稍有畸变的N维环面上。这些环面称为不变环面或卡姆环面。确切些说,相空间分成大小两组体积非零的区域。在大区域中仍然保持着与可积系统类似的环面结构;初始条件如果落入小区域中,运动轨道就会相当不规则地迷走,运动轨道呈现不稳定性。这些小的不稳定区的体积随着ε 趋于零而消失,但只要ε 不为零,它们的体积就是有限的。这说明只有低阶(看来小于4阶)共振才有危险性,高阶共振不影响微扰级数的收敛性。低阶共振的区域在相空间中是彼此隔开的,只有参数ε足够大时,它们才会互相重叠,导致混沌运动。进一步的研究发现无论破坏任何一个卡姆条件,运动图像都会变得更为混沌。轨道的不稳定性是力学系统运动中出现随机性、不可预言性和混沌的原因。卡姆定理通过对弱不可积系统运动稳定性条件的证明,说明了三维以上非线性系统的运动轨道出现混沌现象具有普遍性。这对于突破牛顿力学决定论的思想框架具有重要意义,也丰富了系统学的内容。