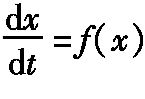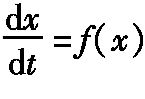词条	相轨线
释义	相轨线 数理化力学卷 相轨线　　从运动的观点考察微分方程 　　(x为n维空间的向量)把t视为时间,x视为空间的点,则方程确定一个速度场,f(x)表示速度向量。已给初始时刻t0和初始点x0,这速度场决定唯一的一个运动,其运动规律由x=x(t;t0,x0)给出,可视为n维空间中一条曲线的参数方程。该空间称为“相空间”,该曲线称为“相轨线”。如果存在T>0,使得对于一切t,成立x(t+T;t0,x0)=x(t;t0,x0),则此曲线称为“闭轨线”。n=2时的相空间称为相平面。满足f(x0)=0的点x0称为方程的奇点。平面上微分方程的奇点有结点、鞍点、焦点和中心等。 出处：数理化力学卷 • 数　　学 • 数学分析
随便看	█ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ ██ █

百科全书收录258893条中英文百科知识，基本涵盖了大多数领域的百科知识，是一部内容开放、自由的电子版百科全书。