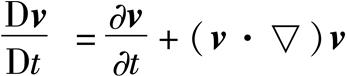
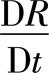 。
。其中,▽是哈密顿算子,在直角坐标系中,。例如在流场中,质点速度v的随体导数的表达式为:
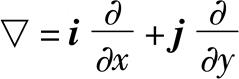
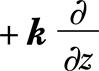 。式中,
。式中,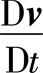 为质点速度的随体导数,也就是它的加速度;
为质点速度的随体导数,也就是它的加速度;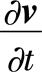 称为“当地加速度”,也称“局部加速度”,表示空间固定点处速度的变化率;(v·▽)v称为“迁移加速度”,也称“位变加速度”,表示由于质点空间位置的变化而引起的速度变化率。
称为“当地加速度”,也称“局部加速度”,表示空间固定点处速度的变化率;(v·▽)v称为“迁移加速度”,也称“位变加速度”,表示由于质点空间位置的变化而引起的速度变化率。出处:数理化力学卷 • 力 学 • 流体力学
| 词条 | 随体导数 |
| 释义 | 随体导数 随体导数 亦称“质点导数”。流体质点在欧拉场中运动时定义的某物理量R随时间的变化率 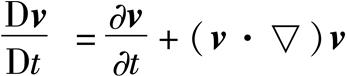 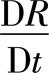 。 。其中,▽是哈密顿算子,在直角坐标系中,。例如在流场中,质点速度v的随体导数的表达式为: 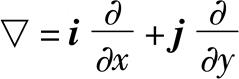 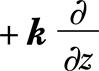 。式中, 。式中,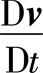 为质点速度的随体导数,也就是它的加速度; 为质点速度的随体导数,也就是它的加速度;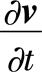 称为“当地加速度”,也称“局部加速度”,表示空间固定点处速度的变化率;(v·▽)v称为“迁移加速度”,也称“位变加速度”,表示由于质点空间位置的变化而引起的速度变化率。 称为“当地加速度”,也称“局部加速度”,表示空间固定点处速度的变化率;(v·▽)v称为“迁移加速度”,也称“位变加速度”,表示由于质点空间位置的变化而引起的速度变化率。出处:数理化力学卷 • 力 学 • 流体力学 |
| 随便看 |
百科全书收录258893条中英文百科知识,基本涵盖了大多数领域的百科知识,是一部内容开放、自由的电子版百科全书。