回归分析(卷名:社会学)
regression analysis
一种研究与测度变量之间关系的技术。对具有相关关系的现象,择一适当的数学关系式,用以说明一个或一组变量变动时,另一变量或一组变量平均变动的情况,这种关系式称为回归方程。如果所择关系式是线性的,就称为线性回归分析;反之,则称为非线性回归分析。线性回归是回归分析的基本模型,很多复杂的情况都是转化为线性回归进行处理的,因此线性回归分析并不限于线性模型。回归分析是社会研究中进行定量分析的基本方法,主要解决以下3个方面的问题:①确定几个变量间是否存在相关关系(见相关分析);若存在,则找出它们之间合适的数学表达式。②据一个或几个变量值,预测或控制另一个或几个变量的值,且要知道这种控制或预测可达何种精确度。③进行因素分析,即在共同影响一个变量的多个变量(因素)间,找出主要和次要因素及其相互关系。根据变量的数目,线性回归可分为以下几种。
一元线性回归 建立一元线性回归方程
尳=α+bx来表示两个变量。例如受教育年限与家庭收入之间的关系。式中x是自变量,y是因变量,α是常数,b是回归系数。尳表示当x取某一数值时,根据以上回归方程所计算的对总体y的平均值的估计值。
复回归 用多元线性方程尳=α+b1x1+b2x2+…+bnxn说明因变量y和一组自变量(x1,x2,…xn)。例如,因变量受教育年限y与自变量家庭收入 x1、本人智力因素x2、健康状况x3、社会环境x4、……间的关系。式中x为自变量的个数,尳为x1,x2,…,xn取定值时,总体y的均值估计值。
多变量复回归 建立可表达x个自变量(x1,x2,…,xn)与P个因变量(y1,y2,…,yp)间关系的多元线性方程组
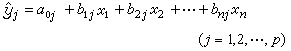 式中尳为根据回归方程预测总体均值的估计值。
式中尳为根据回归方程预测总体均值的估计值。复回归与多变量复回归都可称作多元线性回归。回归分析中的回归系数bi是在除去所有变量的影响后,xi对y的影响,即自变量变化一个单位而使y平均改变的数值。这是对总体作一定的测定后,根据样本观测值采用最小二乘法求得的。在求得一个回归方程后,还要考察它的效果如何,它对变量间关系的描述是否准确,如何利用它根据一组给定的自变量的值预测因变量的值,预测的精度如何。为此,必须对回归进行统计检验。在多元回归中,为了确定自变量的主次和重要性,可先将回归方程标准化,此时的回归系数称为标准回归系数,标准回归系数大的,相应变量的作用越重要。多元回归的另一个问题是,如何在众多的因素中“挑选”变量,以建立对一组观测数据“最优”的方程,包含所有对因变量y显著的自变量和剔除对y不显著的变量,常用的方法为逐步回归,即从一个自变量开始,逐个把变量引入回归方程,随时检验,随时剔除不合格者。多元回归中的自变量,要避免引入相互关系很强的变量。应用线性回归需注意以下几点:①线性回归模型要求因变量与自变量之间的关系是完全的直线关系,这一点在社会现象的研究中有时不能满足。同时,自变量对因变量的影响,除了独立作用外,往往还存在交互作用。在这种情况下,为了能使用线性回归,可以把非线性关系的每一个高次项,以及存在交互作用的乘积项xixj都看作是新的自变量,以满足线性回归对自变量独立作用的要求。
②回归分析要求变量层次都在定距以上(见测量层次)。对于自变量层次是定类的,可采用0,1虚拟变量的方法。如性别是定类变量,为了能使用回归分析,可在方程中设置一个虚拟变量D,并要求:
当 D=0 表示男性;
D=1 表示女性。如果定类变量所分类别不止两类,如文化程度分大学、中学和小学三类,这时可在回归方程中设置2个虚拟变量D1和D2,并要求:
当 D1=0, D2=0 表示小学文化程度;
D1=1, D2=0 表示中学文化程度;
D1=0, D2=1 表示大学文化程度。
③对于定序变量,如果所分等级较少,亦可采用虚拟变量的方法。如所分等级较多,亦可按定距变量处理。
回归分析与相关分析都是研究及测度变量间关系的技术。不同的是,相关分析是探讨变量间关系的密切程度,回归分析则是探求变量间关系究竟为何种形式。两种分析均可不依赖对方而独自进行,通常对关系的两个方面都进行分析。