抽象逼近(卷名：数学)
abstract approximation
在抽象空间中研究逼近论问题。设E是度量空间，ρ是E上的距离，对于确定的元x∈E和集G嶅E，量
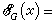
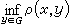为x与G的距离，它自然标志着G对x的逼近程度，称为G对x的最佳逼近值；使等式 ρ(x，y0)=EG(x)成立的元 y0∈G称为 x在 G中的最佳逼近元。对最佳逼近值EG(x)的估计一般仅限于具体的E和G。抽象逼近主要研究下面三个问题：①最佳逼近元y0的存在性；②惟一性；③刻画最佳逼近元的特征。以上说的是集G对元x的逼近，有时给出一族被逼近元F=｛x｝，那么量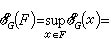
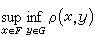就成了标志逼近状态的特征量，称EG(F)为集G对集F的最佳逼近值。有时需要在E的某子集族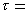
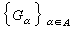中挑选最好的Gα，也即找出Gα0∈τ使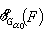
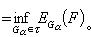
作为逼近集G，有时为E的线性子空间，这时的逼近称为线性逼近；有时为E的凸子集，则称为凸逼近。常见的凸逼近有:有界限逼近，系数有界限的多项式逼近，具有插值约束的逼近，共正逼近，共单调逼近等。
泛函分析是抽象逼近研究的主要工具。例如，若E为线性赋范空间，G是E的线性子空间，那么下述命题（哈恩—巴拿赫定理的推论）可用于导出最佳逼近估计和刻画最佳逼近元的特征：设x∈E\\強，那么①
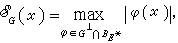式中 BE*为E 的共轭空间E*中的单位球；②y0∈G适合‖y0-x‖=EG(x) 当且仅当存在 ƒ∈E
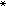使得 ‖ƒ‖=1，ƒ(y)=0（对所有y∈G ），ƒ(x-y0)=‖x-y0‖。