应变张量(卷名：力学)
strain tensor
连续介质力学中度量变形的几何量。在直角坐标系中，未变形物体和已变形物体中线元的平方分别为：
，其中 
和
分别称为柯西应变张量和格林应变张量或右柯西－格林张量。 这两个张量都是对称正定的。另外，
和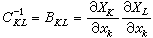
分别称为芬格应变张量或左柯西－格林张量和皮奥拉应变张量。连续介质中两相邻粒子的ds2-dS2可以用来作为变形的度量。可以写作：
，式中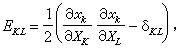
分别称为拉格朗日有限应变张量或格林有限应变张量、欧拉有限应变张量或阿尔曼西有限应变张量。δ
和δ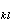
为克罗内克符号。若用位移表示，则得有限变形理论中常用的拉格朗日应变张量和欧拉应变张量：
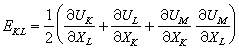和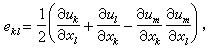
式中UK和uk分别为物质坐标中的和空间坐标中的位移分量。若位移很小，则得无限小变形理论中的拉格朗日和欧拉应变张量：V
和