发酵动力学(卷名：化工)
fermentation kinetics
生化反应工程的基础内容之一，以研究发酵过程的反应速率和环境因素对速率的影响为主要内容。通过发酵动力学的研究，可进一步了解微生物的生理特征，菌体生长和产物形成的合适条件，以及各种发酵参数之间的关系，为发酵过程的工艺控制、发酵罐的设计放大和用计算机对发酵过程的控制创造条件。
在发酵中同时存在着菌体生长和产物形成两个过程，它们都需要消耗培养基中的基质，因此有各自的动力学表达式，但它们之间是有相互联系的，都是以菌体生长动力学为基础的。所谓菌体生长动力学是以研究菌体浓度、限制性基质（培养基中含量最少的基质，其他组分都是过量的）浓度、抑制剂浓度、温度和pH等对菌体生长速率的影响为内容的。在分批发酵中，菌体浓度X，产物浓度P和限制性基质浓度S均随时间t变化（图1）。
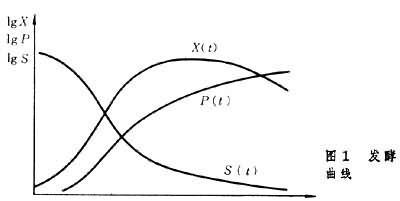
菌体生长可分迟滞、对数、减速、静止、衰退等五个时期。其中菌体的主要生长期是对数期，它的特点是：
式中μ为比生长率，即单位菌体单位时间内的菌体生长量，当基质浓度S下降至一定值后，μ值即随之下降（图2），即进入减速期；随着基质浓度继续下降，菌体的衰老死亡逐步与生长平衡以至超过生长，也即进入静止和衰退期。
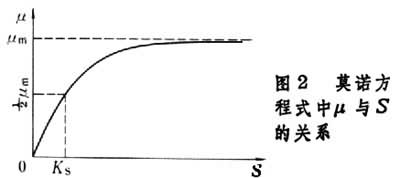
J.莫诺于1949年提出了一个μ与S间的经验关联式，此式被称莫诺方程式：
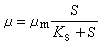式中μm为最大比生长速率， 即不因基质浓度变化而改变的最大μ值;Ks为饱和常数，即在数量上相当于μ=0.5μm时的S值。Ks值愈小，说明在低基质浓度范围中，S对μ愈为敏感，而保持μm的临界S值愈低。在一般情况下，当S＞10Ks时，μ＝μm 当
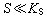时，μ＝(μm/Ks)S。产物的形成常与菌体的生长或浓度有关，典型的关联式为：
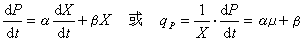式中α、β为常数；qP为比产物形成速率。在限制性基质的消耗和菌体生长间常用下式表示： 
式中YG为菌体得率常数;1/YG则为单纯用于合成单位菌体所耗用的基质量；m为维持系数，即单位菌体、单位时间内耗用于菌体维持生命活动的基质量；qS为比限制性基质消耗速率。若在菌体生长时还伴有产物形成，则
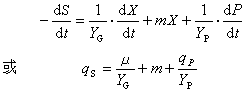式中YP为产物得率系数；1/YP则为单纯用于合成单位产物所耗用的基质量。参考书目
合叶修一、永井史郎著，胡章助等译：《生物化学工程──反应动力学》，化学工业出版社，北京，1984。（合葉修一、永井史郎著：《生物化学工学──反応速度論》，科学技術社，東京，1975。）