李特尔伍德－佩利理论(卷名：数学)
Littlewood-Paley theory
关于lp(p>1)空间中傅里叶级数的理论，1931～1940年由J.E.李特尔伍德、R.E.A.C.佩利首创，后由A.赞格蒙、J.马钦凯维奇等加以发展。它包括以下两个方面。
① 引进两个重要函数（或算子）：
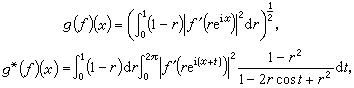式中ƒ（z）=ƒ（reix）是单位圆｜z｜<1内的解析函数，ƒ′(z)是ƒ(z)的导函数。主要结果是：设p>1，那么存在着仅与p有关的常数Ap，Bp，使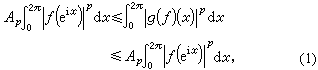
成立。式(1)和(2)的第一个不等式，还要加上ƒ(0)=0的条件。② 三角级数的二进分块。假设φ(x)为实值函数，并且φ(x)∈lp(0，2π)，又设φ(x)的傅里叶级数
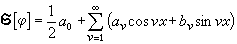。 (3)把(3)分成如下的三角多项式块：
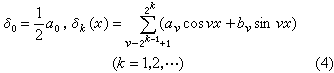叫做三角级数(3)的二进分块。从(1)可以得到以下的结论：存在常数Ap(p>1)，使
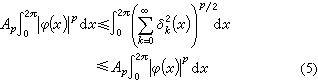不等式(5)是研究lp空间中傅里叶级数的基本工具，它的作用相当于刻画l2(0，2π)空间特征性质的帕舍伐尔等式：设ƒ∈l2（0，2π），又设ƒ的傅里叶级数
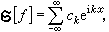那么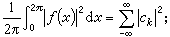
(6)反之，一个三角级数
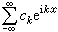的系数满足条件
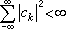时，它就是l2(0，2π)空间中某函数的傅里叶级数。这就是说，三角级数系数的模的大小，能够确定它是否属于l2(0，2π)。对lp(0，2π)，p≠2，类似的问题，复杂得多了。下面是一个例子。任取一个函数ƒ0(x)∈lp（0，2π） (1<p<2)，并设
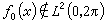，假如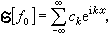
那么可以证明，当随机地取±号时，级数
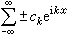“基本上”(以概率1)都不是傅里叶级数。这说明，不可能期望以三角级数的系数的大小来刻画lp(p≠2)空间中函数的特征性质。李特尔伍德－佩利理论正是从这个目的出发去研究lp空间的。上述①中的g、g*函数，以及②中对三角级数的二进分块，都是研究lp空间的重要工具。李特尔伍德-佩利理论的建立，在很大程度上依靠了复变函数论中解析函数的许多重要性质。但是，多元复变函数论的情况很不一样，影响了李特尔伍德-佩利理论在高维空间的推广。1952年出现了考尔德伦－赞格蒙研究高维空间奇异积分的奠基性论文，其中采用的实变函数论方法，对研究高维空间很有成效。在他们影响下，E.M.施坦把李特尔伍德-佩利理论的g函数与Η.Η.卢津的面积函数s推广到高维空间，并建立了相应的定理。1961年，斯坦又把g*函数推广到高维空间，他是利用调和函数来建立的，这些函数已经成为高维空间中傅里叶分析的基本工具。
参考书目
E.M.Stein，Singular Integrals and Differentia-bility of Functions，Princeton Univ. Press， Princeton，1970.