价键理论(卷名：化学)
valence-bond theory
一种获得分子薛定谔方程近似解的处理方法，也称电子配对法。是历史上最早发展起来的化学键理论，它主要描述分子中的共价键和共价结合，其核心思想是电子配对形成定域化学键。
简史 1927年德国物理学家W.H.海特勒和F.W.伦敦首次完成了氢分子中电子对键的量子力学近似处理，这是近代价键理论的基础。美国理论化学家J.C.斯莱特和L.C.鲍林把它推广应用于较复杂的分子。这个理论的特点在于强调分子中电子的定域性质，共价键是由原子的价电子交换而形成。
海特勒－伦敦方法处理氢分子 氢分子的哈密顿算符是：
式中rA1、rB1为核A、B与电子1之间的距离；r12为两个电子之间的距离；RAB为两个原子核之间的距离……(图1)；
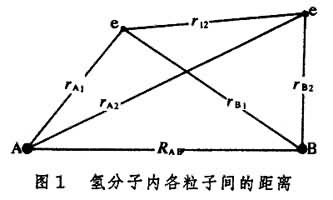1／RAB表示两个原子核之间的势能（氢核和电子电荷皆为 1基本电荷单位）；1/rA1、1/rB1、…也是势能；墷2是拉普拉斯算符。海特勒－伦敦方法的要点在于如何恰当地选取基态H2的近似波函数Ψ(1，2)（或称尝试波函数），然后用变分公式使氢分子能量 E为最低（假定Ψ是归一化的）：
式中*表示复数共轭。考虑两个氢原子组成的体系，若两个氢原子A(有电子1)和B(有电子2)的基态波函数为:φA(1)＝π-1/2exp(-rA1)
φB(2)＝π-1/2exp(-rB2)假如两个氢原子相距很远，那么体系波函数是：
Φ1(1，2)＝φA(1)φB(2)实际上两个电子是不可区分的。同样合适的函数是：
Φ2(1，2)＝φB(1)φA(2)两个函数Φ1和Φ2都对应相同的能量。海特勒和伦敦就取两个函数的等权线性组合作为H2的变分函数:
Ψ(1，2)＝c1Φ1+c2Φ2解久期方程得c1＝±c2，波函数和能量是：
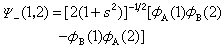
式中 
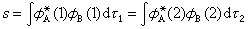s称原子轨道的重叠积分。算出能量公式中各项，积分得：
式中Q、J、s都是R的函数。若用ΔE±表示分子能量与两个分离原子能量之差（图2）：
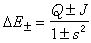ΔE±就是分子相对于分离原子能量为零时的能量。因为H11和H12都是负量，Ψ+态比Ψ-态能量更低，图2 中ΔE+曲线总处于ΔE-曲线的下面。图中虚线表示实验势能曲线。 ΔE+曲线有极小值，表示形成了稳定的 H2。在平衡核间距 Re＝0.87埃，计算得到离解能De＝3.14电子伏（或称结合能）。与实验值Re＝0.742埃，De＝4.75电子伏略有差异，这反映了海特勒－伦敦法的近似程度。ΔE-在R 减小时一直升高。Ψ+称海特勒-伦敦函数，描述H2基态，Ψ-描述排斥态。若考虑自旋，按照泡利原理，必须使分子波函数对电子交换是反对称的。则Ψ+必须乘以反对称自旋函数而给出自旋单重态：
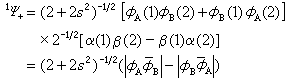Ψ-必须与对称自旋函数相乘得到自旋三重态:
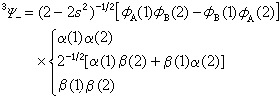1Ψ+态描述了H2的共价键，其中电子自旋是配对的，故称共价键为电子对键。电子密度分布 可以帮助理解共价键的本质。从波函数 Ψ±出发可以计算总电子密度为两个单电子几率密度P±(1)和P±(2)的和乘以电子电量(a，u)。点(x，y，z)处的总电子密度为：
＝
(1)若φA、φB为氢原子的1s轨道，则：
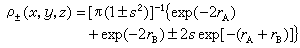式中rA、rB分别表示从点(x，y，z)到核A和B的距离。总电子电荷密度沿核间轴分布如图3。
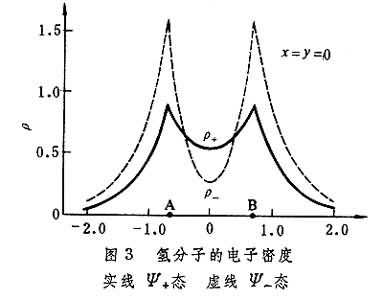由ρ+曲线可见，电子电荷从核外区移向两核之间的区域，相当于电子同时吸引两核，因而降低了势能。由式(1)可知，两原子核愈接近，重叠积分愈大，电荷在核间区愈密集，也即共价键愈牢固（最大重叠原则）。但原子核愈接近，核排斥能和电子排斥能也同时增加，所以氢分子有一稳定的平衡核间距。Ψ-态的电子电荷从核间区移向核外区，使得核间屏蔽减少，能量升高，形成排斥态。电子电荷在两核间密集，影响分子的平均动能〈T〉和平均势能〈V〉。为深入理解共价键的本质，按双原子分子的维里定理计算出2的〈T〉和〈V〉：
又分子总能量E＝〈T〉+〈V〉。如已知E 随R 的改变的(dE/dR)，则得：＜T＞＝-[E+R(dE/dR)]
＜V＞＝2E+R(dE/dR)计算得到的H2基态E、＜T＞、〈V〉都是R 的函数（图4）。
当核间距减少时，电子同核吸引的平均势能降低，但电子的排斥能的平均值增加，核的排斥能也增加。核间距达到某一值（1.401a0， a0为玻尔半径）时，平均总势能达到极小值，电子将在此势阱中运动，此时，dE/dR＝0，平均动能等于平均总势能的负值的一半，氢分子的总能量则为势能平均值的一半。
发展 量子力学对电子对键(或共价键)给出了定量的描述。当然，海特勒-伦敦模型只是最早的一个化学键近似处理。从那以后，已经引入许多相当复杂的近似波函数进行较精确的计算，最精确的计算是在1960～1968年由W.科洛斯和C.C.J.罗特汉完成的，他们使用了一个含有100项的函数（考虑了核运动效应），得到离解能计算值De＝4.74759电子伏，与实验值De＝4.74759电子伏，获得高度的一致。
电子配对法是海特勒－伦敦处理氢分子方法的推广，要点如下：
① 若两原子轨道φA和φB互相重叠，两个轨道上各有一个电子，且电子自旋方向相反，则电子配对给出单重态，形成一个电子对键。
② 两个电子相互配对后，不能再与第三个电子配对，这就是共价键的饱和性。
③ 遵循最大重叠原则，共价键沿着原子轨道重叠最大的方向成键。共价键具有方向性。原子轨道通常在某个特定方向上有最大值，只有在此方向上轨道间才有最大重叠而形成共价键。不同原子轨道有不同的成键能力。在原子轨道φ有最大值的方向上，φ的最大值决定着重叠的大小，因此φ的最大值可做为原子轨道成键能力的度量。鲍林给出s、p、d、f等原子轨道成键能力依次为1、呑、厾、彉。在主量子数相同时，成键能力大的轨道形成的共价键较牢固。
由于异核双原子分子的键有极性，在分子波函数中必须包括离子结构的贡献。如果异核双原子分子AB只有一个电子对键，则有两种可能的离子结构A+B-和A-B+。分子波函数应为：
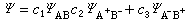实际问题中只有一种离子结构贡献大些，例如氯化氢HCl分子，由H的1S电子与Cl的3pz电子配对形成共价键，描述它的共价结构的函数是：
离子波函数只有：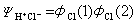
而离子结构
贡献很小，可以略而不计。则HCl的波函数为：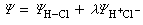
价键理论与化学家所熟悉的经典电子对键概念相吻合，一出现就得到迅速发展。但价键理论计算比较复杂，使得相当长时间内进展缓慢。50年代中国化学家唐敖庆等建议的双电子键函数法也是一项重要进展。60年代，由于发展出直接用基函数计算重叠矩阵和哈密顿矩阵元，不须再使用参数，使得价键理论计算能够程序化。随着计算技术的日益提高，价键理论还将取得新发展。